(a).
(b) Asks you to take the limit of the ratio as x gets large: as it stands as x goes to infinity both the top and bottom go to infinity so the ratio is undefined. the trick is to divide both top and bottom by x. As long as you do exactly the same thing to top and bottom you don't change the ratio.
Doing this gives:
which as x gets large goes to 
.
(a)
This is a straight line problem. You need to write down equations for both additions and depletions.
To find additions equals depletions we set the two equations equal and solve for t.
(b) Note that additions minus depletions per week equals
as a function of t, this is the rate of change in our inventory.
(Here's where I went wrong before!)
The questions asks whether or not we run out of inventory by time 30.
Our change in inventory is the sum (total) of the additions minus the sum (total) of the depletions over the time period, so that we run out if total depletions minus total additions is greater than 8500 (the starting value).
The change over the 30 week time period is the sum of the changes each week. So we have to sum the weekly changes and see if inventory drops by more than 8500.
Treating time as continuous the sum of the weekly changes is given by the
area under the curve of 
(because that tells us how much
inventory changes per week).
To find the area under the curve means we need to integrate, that is to find ( typo, top should be 30, not 3)
The anti-derivative is 
which we evaluate at 30 and 0.
This gives
which means inventory drops by 9000 over the period. We started with 8500 so we do indeed run out.
(a) Note that Q is 2400 and r is 0.002, so the question asks: find the value of t so that
The question says ``find the time'' which means find t. So we simplify and make t the subject of the formula:
So after about 144 days.
(b) The area under the curve of items per day gives ``total production'' so this is an integration problem. That is find
you do this by asking yourself the question: ``what differentiated would give
as the answer''?
The rules of differentiation state that the derivative of
is 
which is correct up to a multiplicative factor.
If we differentiate 
then we get
as the answer, so this must be the anti-derivative.
Generically we take F(b) - F(a) to find the area under the curve.
In this case it's
which simplifies to
Check that it is the right order of magnitude.
(a)
Say we have T trainees and E experienced, then they can do
accounts per day, so we need:
Likewise they cost 
dollars, so we have
(b) The question says ``replace the inequality signs with equality signs and solve''.
So ....
This is a simultaneous equation to solve for T and E.
Multiplying the bottom equation by 50 and subtracting gives:
So that E = 30. Substituting E= 30 back into the top equation gives
So
and thus
(a) Using the hint says we can re-express the original equation as
This is just a regular quadratic.
We find the maxima by differentiating and setting equal to zero:
We now set them equal to zero and solve.
This is a simultaneous equation, rearranging gives:
Taking twice the top from the bottom gives:
so that y = 12.
Substituting this value back into the top equation gives
and therefore x = -20.
The question in fact asks for the values of x and t,
but we know that 
so that at the optimal value of
y we have 
and so 
.
Finally we know it is a maximum by inspecting the function, noting that it is quadratic and remarking on the negative signs of its dominant coefficients.
(b) This is a restricted maximization. we are looking at f(2,t) and finding its max with respect to t.
Using the same trick of substituting in we get
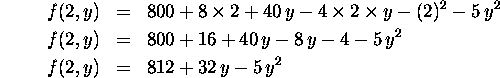
Now differentiate with respect to y to get
so that y = 3.2. Again we know it's a maximum because the function is a quadratic with a negative coefficient on the leading term. Finally solving for t we have t = 10 ln(3.2).
(a) Usable = 
.
To find the max you differentiate, the derivative of usable with respect to x is:
Setting equal to zero gives 
, so 
.
The second derivative is
which must be positive so this is in fact a minimum! Maybe a bad question -- or may need other techniques not covered in our class.
(b)
To show decreasing, show that U(x) has a negative derivative in the range, the derivative of U is
which is indeed negative.
Instantaneous rate of decrease (i.e. the slope) is 
.