MathCamp98 Class 3

Class 3.1 Calculus, introducing the derivative.

Class 3.2 More calculus: putting the derivative to work.

From last time

Exponential growth, geometric series

Functions, straight lines.

Families of functions:

Polynomials:

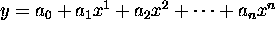
Exponential:

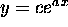
Logarithmic: y = aln(x) + b

Trigonometric:

Motivation for the calculus

Not all functions are straight lines

Their rate of change is not constant

These are the interesting relationships, e.g. diminishing returns

Often looking to find max/mins

Finding where curves cross the x-axis (zero's of a function)

Optimal ... everything (volatility estimators, portfolios, strategies)

Optima usually correspond to derivatives equal to zero, which is why finding zeros is important

Functions

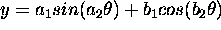
We have the idea of a function. For example a cost function:

D here is termed a ``cost driver''. Changes in the cost driver impact cost.

A simple question: how much does cost change for a small change in the driver (D)?

This is the definition of the marginal cost.

For example, the driver D could be labor hours. If equals 1 then the equation is (anything to the power one is itself)

The left-hand side is measured in Dollars, D is measured in hours, so to make things balance must be in dollars/hour, ie a wage rate.

Look at this cost function.

{\bf Derivatives} give us more information about the function, at what rate it is changing.

You need to get to know the shape/form of a function, it helps you make models and problem solve.

Questions to ask about functions:

• Does it go uphill?
• Downhill?
• How steep is it?
• Does it have maxima/minima?

How do we interpret these changes in practice?

Secant lines

The secant line approximation to a function at a particular point (x).

Graphical view of the secant line.

The tangent line is the limit of the secant line as the "interval" gets smaller.

The derivative is the slope of the tangent line at x.

The derivative of a function at the point x is defined as

In English, the derivative is the "rate of change" of the function.

Ways of writing derivatives (notation - all equivalent):

f'(x).

Two examples to try out the derivative definition.

Example 1, the straight line, .

Example 2, a simple quadratic, .

Notice that the slope is NOT constant, it depends on x itself.

We write

We have just calculated derivatives from "first principles", that is from the definition. Usually we replace this with application of learnt rules, which is what a symbolic math package does.

Rules for our functions:

• For ,
  "Bring down the power, knock the power down 1." So the derivative of is . The derivative of is .
• For the derivative is .
• For the derivative is .
• For y = ln(x) the derivative is .

We can build derivatives up:

A derivative of a sum is the sum of the derivatives. Example

So derivatives of polynomials are easy as they are sums of powers.

The product rule for derivatives:

Example:

The quotient rule for derivatives:

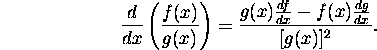
One final rule to add to this group later: the chain rule.

First and second derivatives.

First derivatives, , f'(x). Second derivatives , f''(x).

The second derivative tells you how the "first derivative " is changing.

Example, distance traveled as a function of time.

Interpret the first derivative.

Interpret the second derivative.

Slopes tell you how things are changing:

Picture of curves with different first and second derivatives.

• We have ideas of relationships.
• What are the options for expressing these mathematically?
• What are the implications of our mathematical representation?

Examples.

Liquor store relationships.

Learning curves - what should be going on here?

We learn, get faster, produce quicker or with less inputs.

Mathematical models for representing learning effects.

What about a new product entering the market place? Describe in English how its customer base may change over time.

Maxima and minima

Maxima and minima correspond to values of x where the slope (derivative) of the function is zero.

Steps for finding a min/max (optima).

• Find the derivative of the function.
• Set the derivative equal to zero and solve for x.
• Plug this x into the equation to find y.
• Check the second derivatives to verify max (-ve) or min (+ve).

The liquor store example: how much space should we devote to the wine product to maximize profit? Substituting another item would guarantee a revenue of $50 per foot.

Profit = Revenue - Costs.

Because the cost of displaying a foot of this wine is how much you would receive if you displayed an alternative product.

Example, Page 3 question 3.

3. If x thousand dollars are spent on a promotion, the result is
S(x) = (400,000 x - 200,000)/x additional sales.

   a. (10) Is S(x) an increasing function for all x, as one
would expect in context?

   b. (10)    If each additional unit of sales is worth half a
dollar,  and profit is the worth of additional sales minus the
dollars spent on promotion, what value of x yields the maximum
profit? Recall that x is in thousands of dollars.

Answers:

(a) An increasing function for all x means that the slope is positive for all x. So we figure out the slope by differentiation.

Yes, always positive.

(b) Sales = 0.5 S(x).

Profit = Sales - Promotion.

Profit = 0.5 S(x) - 1000 x.

Differentiate and solve.

Set the derivative equal to zero to get:

So x = 10.

The inventory problem:

Inventory costs are the ordering costs + the carrying costs.

A retailer expects 1200 cases of OJ to be sold in a year.

Each order costs $75.

It costs $8 to carry one case in inventory for 1 year.

Find the order size that minimizes the total inventory costs.

Call x the order size, and r the number of orders made in the year. Then

Minimize this cost ... differentiate and set equal to zero.

If sales goes up by a factor of 4, what happens to order size?

Homework questions.

A set of quick questions to reinforce the days concepts. A calculator will be needed.