Key formulae
Geometric series
Denote the initial value of the series as 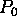

- For a series starting at i = 0 the i-th term is
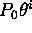 and the sum up to t is
and the sum up to t is
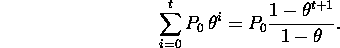

- For a series starting at i = 1 the i-th term is
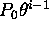 and the sum up to t is
and the sum up to t is
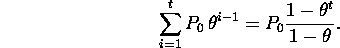

- The sum of an infinite geometric series, so long as
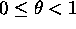 is
is

Discretely compounded interest
Define 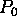 as the principal and
as the principal and 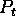 as the value of the investment
at time t.
as the value of the investment
at time t.

-

where r is the interest rate per period and t is the number of
compoundings.

- If the annual rate is r and there are m periods in the year then
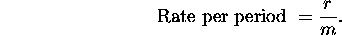

- If the rate per period is
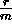 and the interest is compounded for t years then
and the interest is compounded for t years then
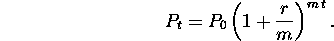
Continuously compounded interest

- A principal amount
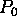 continuously compounded at an interest rate of
continuously compounded at an interest rate of 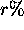 for a time period t is worth at time t
for a time period t is worth at time t

Differentiation

-
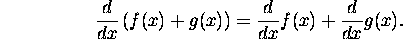

- The product rule:
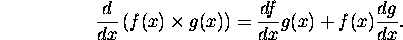

- The quotient rule:
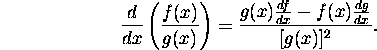

- The chain rule:
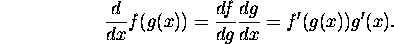
Integration

- The integral of f(x) (area under the curve) with respect to x between the
points x=a and x=b is
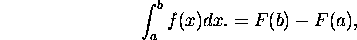
where F is the anti-derivative of f.
Richard Waterman
Sun Aug 9 22:24:45 EDT 1998
![]()
![]()
![]()
![]()
![]() as the principal and
as the principal and ![]() as the value of the investment
at time t.
as the value of the investment
at time t.
![]()
![]()
![]()
![]()
![]()
![]()
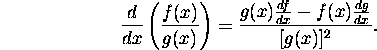
![]()
![]()