Class 3

What you need to have learnt from Class 2.

The second rule of data analysis: always check the residuals.

The regression assumptions.

Consequences of assumption violations.

Diagnosing violations through residual plots.

Categorizing unusual points: leverage, residuals and influence.

Impact of unusual points on the regression.

How important is a point? Remove it and see how your decision changes.

New material for Class 3.

Understanding almost all the regression output

R-squared.

The proportion of variability in Y explained by the regression model.

Answers the question ``how good is the fit''?

Root mean squared error (RMSE).

The spread of the points about the fitted model.

Answers the question ``can you do good prediction''?

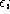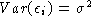Write the variance of the as , then RMSE estimates .

Only a meaningful measure with respect to the range of Y.

A rule of thumb 95% prediction interval: up to the line +/- 2 RMSE (only works in the range of the data).

Confidence interval for the slope.

Answers the question ``is there any point in it all''?

If the CI contains 0, then 0 is a feasible value for the slope, i.e. the line may be flat, that is X tells you nothing about Y.

The p-value associated with the slope is testing the hypothesis Slope = 0 vs Slope 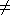0.

Two types of prediction (concentrate on the second)

Estimating an average, ``where is the regression line''?

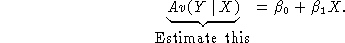
Range of feasible values should reflect uncertainty in the true regression line.

Predicting a new observation, ``where's a new point going to be''?

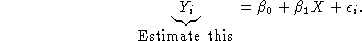
Range of feasible values should reflect uncertainty in the true regression line AND the variability of the points about the line.

What a difference a leveraged point can make.

   From pages 96 and 100.

     Measure      With outlier    Without outlier

     R-squared    0.78            0.075
     RMSE         3570             3634
     Slope        9.75             6.14
     SE(slope)    1.30             5.56

If someone comes with a great R-squared it does not mean they have a great model; maybe there is just a highly leveraged point well fit by the regression line.