Review of QR algorithm

Here is a worked example to illustrate the use of the QR decomposition in solving a least squares equation.

For an matrix X, we want to find an orthogonal (length preserving) matrix Q ( ) such that , where R is a block upper triangular matrix.

Take

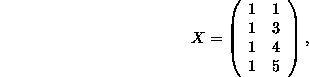
then if Q is such that

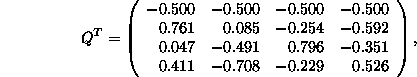
you can verify that

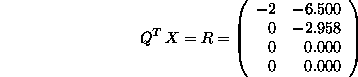
which is block upper triangular as required.

To solve the least squares equation

we can equivalently solve

Take for example

then

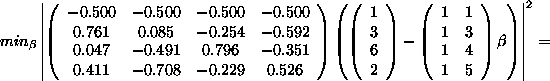
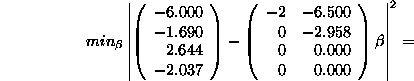
So and . The residual is of length , so that the RMSE =

Orthogonal matrix have the propery that , so that is equivalent to , which is the way one usually sees the QR decomposition.

To summarize, the objective is to decompose a matrix X as where X is , Q is and R is upper triangular, with Q orthogonal.

The S-Plus code to produce these matrices is availble as qr.q.