Stat 601, Fall 2000, Class 1

- Review intro stat ideas

- Change emphasis toward interpretation and practical application

- Learn the software

- Enjoy it

- Course material

- Grading/assessment

- TA's and office hours??

- Evaluations

- Computing

- Good questions

- Insights

- Clarifications

- Tie backs/big picture

- Bad questions

- Missed last class

- Flex muscles
Metaphor; the spoken language, not the grammar.

- Material

- Classes 1-4. Understanding/measuring variability. Why it is important. Factor in variability/uncertainty to the decision making process

- Who cares? The Basel Accord

- Risky investments need higher reserves

- Need to measure risk. e.g. J.P.Morgan

- Risk == volatility of returns

- Volatility == variability

- Classes 5-10. Regression/statistical modeling/forecasting/explaining
variability

- Models

- Stock market

- Market share

- Real estate prices

- What's different? Our model explicitly incorporate variability; don't just get to model the process, get to say how good the model is. Meta-information: statements about the quality oif information.
Value added - the idea of precision.

- What to get out of the course

- Perform statistical analysis - hands on

- No stats background - not math based

- Project, THE learning experience

- PRACTICAL APPLIED MODERN STATISTICS

- Success in the course

- Learn the right questions to ask

- Critical evaluation of another's analysis

- Mastery of stat package

- Confidence to perform analysis/use tools

- Presentation and communication of results

- Guarantee: you will be faced with more data, not less.
This course is about evaluating, summarizing and leveraging information

- Popular quote ``if you can't measure it you can't manage it''
- Key concept: Summarizing data
- Key tool: the Empirical rule
- Key graphics: Histogram and boxplot
Graphics
| Box plot |
Identification of outliers |
| Histogram |
Shape of data, skewness. Outliers |
| Normal quantile plot |
Diagnostic for normality |
| |
CENTER |
SPREAD |
| Sensitive to outliers |
Mean |
Variance/SD |
| Robust |
Median |
IQR |

- Mean = average. True
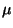 ,
estimated
,
estimated
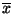

- Median = order the data, the one in the middle. Not standard.

- Variance = average squared distance from the mean. True
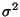 ,
estimated s2
,
estimated s2

- S.D. =
 .
True
.
True 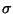 ,
estimated s
,
estimated s

- IQR = 75 pctile - 25 pctile. Not standard.

- Symmetric bell shaped; mean
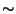 median
median

- Right skew; mean greater than median

- Left skew; mean smaller than median

- Symmetric bell shaped - good news.

- Skewness - watch out!
If data bell shaped and symmetric then say approximately normal.
Key: the mean and standard deviation summarize the data efficiently in
these circumstances.
The EMPIRICAL RULE rule applies when data is approximately normal.
Rule of thumb for normal data - it ties together the mean and standard
deviation, (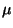 and
and 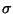 )
into a rule that establishes where most of the data should lie. If the data is outside this range then it's an
``atypical'' observation; in J.P. Morgan's terminology an adverse market move.
)
into a rule that establishes where most of the data should lie. If the data is outside this range then it's an
``atypical'' observation; in J.P. Morgan's terminology an adverse market move.
Special one:
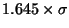 gives a 10% chance of
falling out of the range. That is 5% on each side (tail), one in 20 times
we see the lower event, about 1 trading day a month.
gives a 10% chance of
falling out of the range. That is 5% on each side (tail), one in 20 times
we see the lower event, about 1 trading day a month.

- Summary measures

- Robust vs. Sensitive

- Empirical rule for mound shaped and symmetric data

- Ties together mean and s.d. to help define an ``unusual event''

- Disparate data may be approx normal, ie GMAT and GM

- But not ALL data is normal, ie Eisner's compensation.
2000-09-08
![]() and
and ![]() )
into a rule that establishes where most of the data should lie. If the data is outside this range then it's an
``atypical'' observation; in J.P. Morgan's terminology an adverse market move.
)
into a rule that establishes where most of the data should lie. If the data is outside this range then it's an
``atypical'' observation; in J.P. Morgan's terminology an adverse market move.
![]() gives a 10% chance of
falling out of the range. That is 5% on each side (tail), one in 20 times
we see the lower event, about 1 trading day a month.
gives a 10% chance of
falling out of the range. That is 5% on each side (tail), one in 20 times
we see the lower event, about 1 trading day a month.