Stat 601, Fall 2000, Class 10

What you need to have learnt from Class 9

The partial F test, and why you would use it.

 The partial-F 
    \begin{verbatim}

        /    2                 2     \     /Number of 
       |    R        -        R      |    / variables
        \    BIG               SMALL /   / in the subset.
        __________________________________________________________________

         /                      2     \     / Number of observations
        |    1        -        R      |    / minus number of parameters
         \                      BIG   /   / in Big model. (inc. intercept).

Example

Page 152 of the Case Book. Testing

$$H_0: \beta_2 \& \beta_3 = 0 \quad v. \quad H_1: \beta_2 \mbox{\rm or} \beta_3 \ne 0.$$

Regression for time series

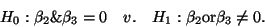
Objective: model a time series.

Example: Model default rates on mortgages as a function of interest rates.

Problem: Time series often have autocorrelated error terms which violates the standard assumption of independence.

Definition: Autocorrelation - successive error terms are dependent (see p.41 and p.300 of the Bulk Pack).

Diagnostics.

Key graphic - residuals plotted against time. Tracking in the residual plots.

Look at the Durbin-Watson statistic. Less than 1.5 or over 2.5 suggests a problem.

Correlation of the residuals is roughly 1 - DW/2.

Consequences of positive autocorrelation:

Over-optimistic about the information content in the data.

Standard errors for slopes too small, confidence intervals too narrow.

Think variables are significant when really they are not.

False sense of precision.

Fix ups.

Use differences of both Y and X, not raw data (pp.326-327).

Include lagged residuals in the model (p. 309).

Include lag Y in the model (as an X-variable p.331).

Benefits of differencing.

Often reduces autocorrelation.

Can reduce collinearity between X-variables.

Two transforms

Linear

$$Y = \beta_0 + \beta_1 X + \epsilon,$$

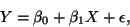
or, say X is in grams and we re-express as kilos:

$$Y = \beta_0 + 1000 \times \beta_1 X/1000 + \epsilon.$$

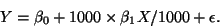
Essentially the same equation but the original 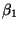$\beta_1$ would be 1000 times larger in the second equation.

Say we transform Y but not X, Y is originally in cm, but we divide by 100 to get to meters:

$$Y/100 = \beta_0/100 + (\beta_1/100) X + \epsilon/100.$$

Notice how the slope and intercept change. The RMSE would fall by a factor of 100 too.

Log transforms

Note: all percent change interpretations for log transforms are valid only if the percent change considered is small. The smaller it is the better the approximation.

Four cases:

$Av(Y\vert X) = \beta_0 + \beta_1 X.$

$Av(Y\vert X) = \beta_0 + \beta_1 ln(X).$

$Av(ln(Y)\vert X) = \beta_0 + \beta_1 X.$

$Av(ln(Y)\vert X) = \beta_0 + \beta_1 ln(X).$

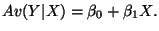
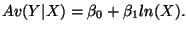
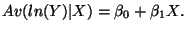
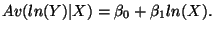
Four respective interpretations for 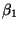$\beta_1$:

For a 1 unit change in X, the average of Y changes by $\beta_1$.

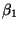For a 1 percent change in X, the average of Y changes by $\beta_1/100$.

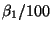For a 1 unit change in X, the average of Y changes by 100 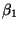$\beta_1$ percent.

For a 1 percent change in X, the average of Y changes by 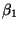$\beta_1$ percent - the economist's elasticity definition.

Plug in numbers if in doubt: take 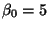$\beta_0 = 5$ and $\beta_1 = 0.5$.

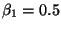Av(ln(Y)|X) = 5 + 0.5 ln(X).

Calculate Av(ln(Y)) at X = 100: 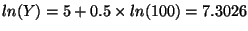$ln(Y) = 5 + 0.5 \times ln(100) = 7.3026$, so Y = 1484.13

Increase X by 1% (X = 101) and recalculate: 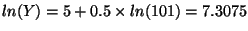$ln(Y) = 5 + 0.5 \times ln(101) = 7.3075$, so Y = 1491.53

Y has gone from 1484.13 to 1491.53, or in percent terms: (1491.53 - 1484.13)/1484.13 = 0.00498 = 0.498%, which is approximately 0.5%.

Plug in numbers if in doubt: take 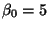$\beta_0 = 5$ and $\beta_1 = 0.03$.

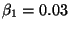Av(ln(Y)|X) = 5 + 0.03 X.

Calculate Av(ln(Y)) at X = 50: 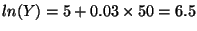$ln(Y) = 5 + 0.03 \times 50 = 6.5$, so Y = 665.14

Increase X by 1 (X = 51) and recalculate: 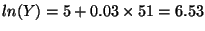$ln(Y) = 5 + 0.03 \times 51 = 6.53$, so Y = 685.40

Y has gone from 665.14 to 685.40, or in percent terms: (685.40 - 665.14)/665.14 = 0.0305 = 3.05%, which is approximately 3%.