Stat 601, Fall 2000, Class 2

- Summary measures; mean, median,variance,sd,IQR

- Graphical summaries/diagnostics; histogram,boxplot,normal quantile plot

- If approx normal then can use empirical rule

- What is the Empirical rule?

- Often data is approx normal - but not always

- Tracking sample means and standard deviations: x-bar and s-charts. Setting control limits

- The standard error of the mean;
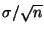

- The Central Limit Theorem

- Confidence intervals

- Using a confidence interval to make a decision

- Assumptions and their role in analysis
ShaftXtr.jmp
Monitor a production process assuming observations are independent.

- Achieve this by placing control limits

- How to choose limits - can use empirical rule on sample means

- In control: mean and variance stable over time

- Capable: process meets specs

- E.R. needs to know s.d. of the sample means

- SD of
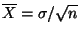 where n is number of
observations in sample mean
where n is number of
observations in sample mean

- Can use overall sample mean +/- 3
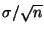 as "3 sigma
limits"
as "3 sigma
limits"

- Chances a particular observation is outside these limits if process is
in control is 1 -.997 (from ER), ie small

- Unlikely evens signal something is wrong -> take action
- Sample means are less variable than raw data
- SE(
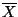 )
=
)
=
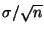 where
where 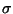 is the true s.d. of a single observation and n is the number of observations in the sample mean
is the true s.d. of a single observation and n is the number of observations in the sample mean

- Sample means are approximately normally distributed. (see p.66 of CaseBook)

- E(
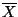 )
=
)
= 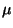 .
.

- Var(
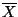 )
=
)
=
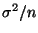 .
.

- s.d.(
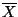 )
= SE(
)
= SE(
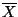 )
=
)
=
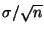 .
.

- Because sample means are approx. normal can use Empirical Rule on them.

- Two types

- X-bar chart; track sample means

- s-chart; track sample standard deviations

- Setting the control limits - two ways (JMP gives choice);

- From the engineer; use their specs to create limits

- From the data; use overall sample mean and overall sample variance
plus the Empirical Rule to create limits (typically 3-sigma)
Two examples
 ShaftXtr.jmp A well behaved process -- in control.
ShaftXtr.jmp A well behaved process -- in control.
 CarSeam.jmp A process that fails to meet engineers specs.
CarSeam.jmp A process that fails to meet engineers specs.
 CompChip.jmp A process that breaks down.
CompChip.jmp A process that breaks down.

- S-charts are usually one-sided in manufacturing

- Dealing with miracles; someone has to win the lottery but the same person should not win it three times in a row. (p.63 of CaseBook)

- Daily means, weekly means, monthly means or WHAT? (p.79 of CaseBook)

- What is it?

- 1. A range of feasible values for an unknown population parameter, e.g.
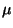 or
or 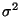

- 2. A statement conveying the confidence that the range of feasible values really does include the unknown population value

- Where does it come from?

- Inverting the Empirical rule

- If 95% of the time the sample mean is within +/- 2 standard errors from
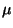 ,
then 95% of the time the true
,
then 95% of the time the true 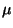 is within +/- 2 standard errors from the sample mean
is within +/- 2 standard errors from the sample mean

- Why is it important?

- Move away from a single ``estimate'' to a range of values, which is more realistic

- Get to make the meta-level statement - our confidence
about the first statement

- How do I use it to make a decision?

- Example, is 812 a feasible value for the true mean?

- Answer: look to see if 812 lies in the confidence interval

- If it's in the interval then it's a feasible value

- If it's outside the interval then it is not feasible
 ShaftXtr.jmp A confidence interval for the population mean.
ShaftXtr.jmp A confidence interval for the population mean.
 CompPur.jmp A confidence interval for the intent to purchase.
CompPur.jmp A confidence interval for the intent to purchase.
2000-09-09
![]()
![]()
![]()
![]()
![]()
![]()
![]() where n is number of
observations in sample mean
where n is number of
observations in sample mean
![]()
![]() as "3 sigma
limits"
as "3 sigma
limits"
![]()
![]()
![]() )
=
)
=
![]() where
where ![]() is the true s.d. of a single observation and n is the number of observations in the sample mean
is the true s.d. of a single observation and n is the number of observations in the sample mean
![]()
![]()
![]() )
=
)
= ![]() .
.
![]()
![]() )
=
)
=
![]() .
.
![]()
![]() )
= SE(
)
= SE(
![]() )
=
)
=
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ShaftXtr.jmp A well behaved process -- in control.
ShaftXtr.jmp A well behaved process -- in control.
![]() CarSeam.jmp A process that fails to meet engineers specs.
CarSeam.jmp A process that fails to meet engineers specs.
![]() CompChip.jmp A process that breaks down.
CompChip.jmp A process that breaks down.
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]()
![]() ,
then 95% of the time the true
,
then 95% of the time the true ![]() is within +/- 2 standard errors from the sample mean
is within +/- 2 standard errors from the sample mean
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ShaftXtr.jmp A confidence interval for the population mean.
ShaftXtr.jmp A confidence interval for the population mean.
![]() CompPur.jmp A confidence interval for the intent to purchase.
CompPur.jmp A confidence interval for the intent to purchase.