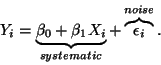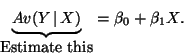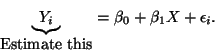Stat 601, Fall 2000, Class 6

- Fitting equations to data, least squares

- Assumptions in regression

- Understanding outliers in regression

- Prediction and confidence intervals
Once we have an equation we can summarzie and exploit fit:

- Graphically summarize

- Interpolate

- Forecast/extrapolate (with caution)

- Leverage the equation, marginal this, that ...
The classical definition of the ``best'' line:

- Find the
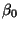 and
and 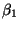 that minimize
that minimize
Call the minimizers
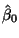 and
and
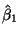 .
.

- In English, the ``best line'', minimizes the sum of vertical distances
squared, the Least Squares Line.

- Sometimes, we may fit a line on a transformed scale, then back-transform, which gives ``best fitting'' curves.

- The cardinal rule of data analysis: always, always plot your data.

- Our model:
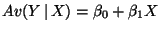 .
.

- In the equation
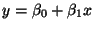

- Intercept:
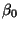 :
the value of y, when x = 0.
:
the value of y, when x = 0.

- Slope:
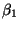 :
the change in y for every one unit change in x. Always
understand the units on
:
the change in y for every one unit change in x. Always
understand the units on 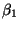 .
.

- The
interpretation of the slope in a ln(x) transformed model as a
percentage change (see p.21 of the bulkpack).
In this section, you must understand the idea of the residual:
Residual = the difference between what we observe (yi), and what we expect
(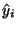 )
under the model.
)
under the model.
You must also understand the difference between the
``true regression line''
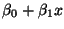 ,and the ``estimated
regression line''
,and the ``estimated
regression line''
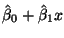 .
It's like the
difference between the population and sample means.
.
It's like the
difference between the population and sample means.

- The second rule of data analysis: if it's measured against time,
plot against time.

- The third rule of data analysis: always check the residuals.

- Regression assumptions and how to check for them.
-
- So far we have thought of our model as the rule that relates the
average value of Y to X, that is
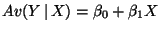 .
.
-
- The process that generates the data, the actual Y-variables
themselves is often modeled as
-
- That is we think of the data as coming from a two part process,
a systematic part and a random part (signal plus noise). The noise
part is sometimes due to measurement error and other times
interpreted as all the important variables that should have been
in the model but were left out.
-
- The regression assumptions:

-
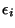 are independent.
are independent.

-
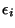 are mean zero and have constant variance,
are mean zero and have constant variance,
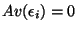 and
and
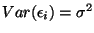 for all
i. (constant variance)
for all
i. (constant variance)

-
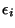 are approximately normally distributed.
are approximately normally distributed.
-
- Consequences of violation of the assumptions:

- If positive autocorrelation then we are over-optimistic about
the information content in the data. We think that there is less
noise than there really is. Confidence intervals too narrow.

- Non-constant variance:

- Incorrectly quantify the true uncertainty.

- Prediction intervals are inaccurate.

- Least squares is inefficient: if you understood the structure of
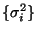 better you could get better estimates of
better you could get better estimates of
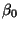 and
and 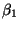 .
.

- If
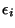 are symmetric then normality assumption is not
a big deal. If
are symmetric then normality assumption is not
a big deal. If
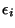 are
really skewed and you only have a small amount of data then it is
all up the creek.
are
really skewed and you only have a small amount of data then it is
all up the creek.

- Since the assumptions are on the error term, the
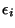 ,
we have to check them by looking at the ``estimated errors'', the
residuals.
,
we have to check them by looking at the ``estimated errors'', the
residuals.

- Note that
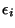 is the distance from the point to the
true line.
is the distance from the point to the
true line.

- But the residual is the distance from the point to the
estimated line.

- Identifying unusual points; residuals, leverage and influence.

- Points extreme in the X-direction are called points of high
leverage.

- Points extreme in the Y-direction are points with BIG residuals.

- Points to watch out for are those that are high leverage and
with a BIG residual. These are called influential
points. Deleting them from the regression can change everything.

- R-squared.

- The proportion of variability in Y explained by
the regression model.

- Answers the question ``how good is the fit''?

- Root mean squared error (RMSE).

- The spread of the points about the fitted model.

- Answers the question ``can you do good prediction''?

- Write the variance of the
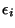 as
as
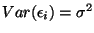 ,
then RMSE estimates
,
then RMSE estimates 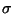 .
.

- Only a meaningful measure with respect to the range of Y.

- A rule of thumb 95% prediction interval: up to the line +/-
2 RMSE (only works in the range of the data).

- Answers the question ``is
there any point in it all''?

- If the CI contains 0, then 0 is a feasible value for the
slope, i.e. the line may be flat, that is X tells you nothing
about Y.

- The p-value associated with the slope
is testing the hypothesis Slope = 0 vs Slope
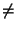 0.
0.

- Estimating an average, ``where is the regression line''?
Range of feasible values should reflect uncertainty in the
true regression line.

- Predicting a new observation, ``where's a new point going to
be''?
Range of feasible values should reflect uncertainty
in the true regression line AND the variability of the
points about the line.

-
From pages 90 and 94.
Measure With outlier Without outlier
R-squared 0.78 0.075
RMSE 3570 3634
Slope 9.75 6.14
SE(slope) 1.30 5.56
If someone comes with a great R-squared it does not mean they
have a great model; maybe there is just a highly leveraged point
well fit by the regression.
2000-11-03
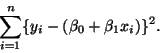
![]() )
under the model.
)
under the model.
![]() ,and the ``estimated
regression line''
,and the ``estimated
regression line''
![]() .
It's like the
difference between the population and sample means.
.
It's like the
difference between the population and sample means.