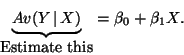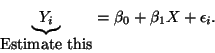Stat 601, Fall 2000, Class 7




What you need to have learnt from Class 6

*
Understand the uses of curve fiting
*
Know the interpretation of the Least Squares fit
*
Understand residuals
*
Know the regression assumptions
*
Classify unusual points

New material for Class 7

*
R2
*
RMSE
*
Confidnce and prediction intervals
*
Introduction to multiple regression

Understanding almost all the regression output

*
R-squared.
*
The proportion of variability in Y explained by the regression model.
*
Answers the question ``how good is the fit''?
*
Root mean squared error (RMSE).
*
The spread of the points about the fitted model.
*
Answers the question ``can you do good prediction''?
*
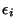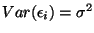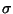Write the variance of the $\epsilon_i$ as $Var(\epsilon_i) = \sigma^2$, then RMSE estimates $\sigma$.
*
Only a meaningful measure with respect to the range of Y.
*
A rule of thumb 95% prediction interval: up to the line +/- 2 RMSE (only works in the range of the data).

Confidence interval for the slope

*
Answers the question ``is there any point in it all''?
*
If the CI contains 0, then 0 is a feasible value for the slope, i.e. the line may be flat, that is X tells you nothing about Y.
*
The p-value associated with the slope is testing the hypothesis Slope = 0 vs Slope 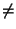$\ne$ 0.

Two types of prediction (concentrate on the second)

*
Estimating an average, ``where is the regression line''?

\begin{displaymath}\underbrace{Av(Y\,\vert\,X)}_{\mbox{Estimate this}} = \beta_0 + \beta_1 X.\end{displaymath}

Range of feasible values should reflect uncertainty in the true regression line.
*
Predicting a new observation, ``where's a new point going to be''?

\begin{displaymath}\underbrace{Y_i}_{\mbox{Estimate this}} = \beta_0 + \beta_1 X + \epsilon_i.\end{displaymath}

Range of feasible values should reflect uncertainty in the true regression line AND the variability of the points about the line.

What a difference a leveraged point can make

* 
   From pages 90 and 94.

     Measure      With outlier    Without outlier

     R-squared    0.78            0.075
     RMSE         3570             3634
     Slope        9.75             6.14
     SE(slope)    1.30             5.56

If someone comes with a great R-squared it does not mean they have a great model; maybe there is just a highly leveraged point well fit by the regression.

Multiple regression

*
Making more realistic models with many X-variables - multiple regression analysis.
*
The fundamental differences between simple and multiple regression.
*
The X-variables may be related (correlated) with one another.
*
Consequence: looking at one X-variable at a time may present a misleading picture of the true relationship between Y and the X-variables.
*
The difference between marginal and partial slopes. Marginal: the slope of the regression line for one X-variable ignoring the impact all the others. Partial: the slope of the regression line for one X-variable taking into account all the others. Recall the death penalty example.
*
Key graphics for multiple regression.
*
The leverage plot. A ``partial tool'': the analog of the scatterplot for simple regression. It lets you look at a large multiple regression one variable at a time, in a legitimate way (controls for other X-variables). Potential uses:
*
Spot leveraged points.
*
Identify large residuals.
*
Diagnose systematic lack of fit, i.e. spot curvature which may suggest transformations.
*
Identify heteroscedasticity.
*
The scatterplot matrix. A ``marginal tool'': presents all the two-variable (bivariate) relationships. Potential uses:
*
Identify collinearity (correlation) between X-variables.
*
Identify marginal non-linear relationships between Y and X-variables.
*
Determine which X-variables are marginally most significant (thin ellipses).
*
Facts to know.
*
R-squared always increases as you add variables to the model.
*
RMSE does not have to decrease as variables are added to the model.
*
Model building philosophy in this course.
*
Keep it as simple as possible (parsimony).
*
Make sure everything is interpretable (especially any transformations).
*
After having met the above criteria go for biggest R-squared, smallest RMSE and the model that makes most sense (signs on regression slopes).



2000-11-09