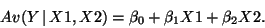Stat 601, Fall 2000, Class 8

What you need to have learnt from Class 7

What is multiple regression?

The model:

$$Av(Y\,\vert\, X1,X2) = \beta_0 + \beta_1 X1 + \beta_2 X2.$$

The picture

The interpretation of the partial slopes in multiple regression. Example: if we have two X variables X1 and X2 then the partial slope of X1 is interpreted as ``the change in Y for every one unit change in X1 holding X2 constant''.

The essential difference between multiple regression and simple (one X) regression - the fact that in multiple regression the X's may be correlated which implies that looking at partial slopes or marginal slopes can lead to different decisions.

What makes a good model (it can depend on your objectives).

What can be learnt from a leverage plot.

New material for Class 8. Collinearity, Hypothesis testing and categorical variables

Collinearity

Definition: correlation between the X-variables.

Consequence: it is difficult to establish which of the X-variables are most important (they all look the same). Visually the regression plane becomes very unstable (sausage in space, legs on the table).

Diagnostics:

Thin ellipses in the scatterplot matrix. (High correlation.)

Counter-intuitive signs on the slopes.

Large standard errors on the slopes (there's little information on them).

Collapsed leverage plots.

High Variance Inflation Factors. The increase in the variance of the slope estimate due to collinearity.

Insignificant t-statistics even though over all regression is significant (ANOVA F-test).

Fix ups:

Ignore it. OK if sole objective is prediction in the range of the data.

Combine collinear variables in a meaningful way.

Delete variables. OK if extremely correlated.

Hypothesis testing in multiple regression. Three flavors. They all test whether slopes are equal to zero or not. They differ in the number of slopes we are looking at simultaneously.

Test a single regression coefficient (slope).

Look for the t-statistic.

The hypothesis test in English: does this variable add any explanatory power to the model that already includes all the other X-variables?

Small p-value says YES, big p-value says NO.

Test all the regression coefficients at once.

Look for the F-statistic in the ANOVA table.

The hypothesis test in English: do any of the X-variables in the model explain any of the variability in the Y-variable?

Small p-value says YES, big p-value says NO.

Note that the test does not identify which variables are important.

If you answer this question as NO then it's back to the drawing board - none of your variables are any good!

Test a subset of the regression coefficients (more than one, but not all of them - the Partial F-test).

It's no use looking for this one on the output. You have to calculate it yourself. See formula on p. 152 of the BAUR.

The test in English: do any of the X-variables in the subset under consideration explain any of the variability in Y?

We use a rule of thumb for this one. If the partial F is less than one then you can be sure that the answer is NO. If it is greater than 4 then you can be sure that the answer is YES. If it is in between 1 and 4 then we will let it be a judgment call.

Must be able to answer this question: ``why not do a whole bunch of t-tests rather than one partial F-test?'' Answer: the partial F-test is an honest simultaneous test (see p. 135 of Bulk Pack).

Categorical variables as predictors

Start with 2 groups in the categorical variable, more than two groups is covered in class 9.

Key fact: When JMP compares two groups in a regression, the comparison is between each group and the average of the two groups. In fact JMP only compares one group to the average, but if you know that one group is three below the average then you know that the other group must be three above the average, so it's not a big deal.

Parallel lines regression - allowing different intercepts for the two groups.

Declare the variable as NOMINAL.

Add it just like any other X-variable.

Including the categorical variable allows you to fit a separate line to each group so that you can compare them.

Recognize that the comparison is between each group and the average of the two groups.

Recognize that the lines are forced to be parallel.

The ``slope'' estimate on the categorical variable is the difference between one group and the average of the two groups for the estimated Y-value.

The height difference between the parallel lines is given by twice the estimated slope for the categorical variable.

Non-parallel lines regression - allowing different intercepts and different slopes for each group.

Declare the categorical variable as NOMINAL.

Add it just like any other X-variable but also add the cross product term. Cross product terms are sometimes known as interaction terms.

The ``slope'' on the categorical variable tells you the difference between intercepts, comparing each group to the average of the two groups.

The ``slope'' on the cross product term tells you the difference between slopes for the two groups, comparing each group slope to the average of the group slopes.