Class 2

What you need to know from last time

Summary measures; mean, median,variance,sd,IQR

Graphical summaries/diagnostics; histogram,boxplot,normal quantile plot

If approx normal then can use empirical rule

What is the Empirical rule?

Often data is approx normal - but not always

Two parts to todays class

Covariance and correlation

Tracking means and variances

Covariance and correlation

Summary measures for 2 variables.

Covariance - measuring the linear relationship

Correlation - measuring the linear relationship on a unitless scale: -1 <= Correlation <= 1

-1 is perfect negative dependence

+1 is perfect positive dependence

When data is Normal then Correlation = 0 is equivalent to independence

Can compare two correlations, but not typically two covariances.

            
Corr(X,Y) = Cov(X,Y)/Sqrt{Var(X) * Var(Y)}     

Cov(X,Y) = Corr(X,Y) * Sqrt{Var(X) * Var(Y)}

Key application: building low risk portfolios.

Idea: buying instruments that move in opposite directions can lower portfolio variability dramatically

Example

StockRet.jmp

Theory - population quantities - true but unknown

Practice - use sample statistics

Finance arithmetic

Average of sum is sum of averages

X is return on IBM, Y is return on Walmart

Portfolio is X + Y

E[X + Y] = E[X] + E[Y]

Variance of sum is sum of variances only if X and Y are uncorrelated

Var(X + Y) = Var(X) + Var(Y)

Variance of sum is sum of variances PLUS 2 * sum of all covariance pairs

Var(X + Y) = Var(X) + Var(Y) + 2 * Cov(X,Y)

All details in course pack

Toy example:

Two instruments X and Y.

Make a portfolio, with weights w1 and w2 = 1 - w1.

Say Var(X) = Var(Y) = 1.

How does the portfolio variance change with w1 and ?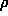

Down load image or copy in class.

Part 2 of class

Monitoring the mean and variance of a process

Example

ShaftDia.jmp

Objective

Monitor a production process assuming observations are independent.

Achieve this by placing control limits

How to choose limits - can use empirical rule on sample means

Sample means are approx normal (central limit theorem -- more later)

In control: mean and variance stable over time

Capable: process meets specs

E.R. needs to know s.d. of the sample means

SD of 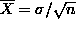where n is number of observations in sample mean

Can use overall sample mean +/- 3 * 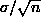as "3 sigma limits"

Chances a particular observation is outside these limits if process is in control is 1 -.997 (from ER), ie small

Unlikely events signal something is wrong -> take action