Class 3
Discuss write-up for assignment 1.
What you need to know from last time
 Summary measures; covariance and correlation
Summary measures; covariance and correlation
 Finance arithmetic, basic probability (assigned reading)
Finance arithmetic, basic probability (assigned reading)
 Capable process - meets engineers specs.
Capable process - meets engineers specs.
 In control process - mean and variance stable over time
In control process - mean and variance stable over time
Todays class
 The standard error of the mean;
The standard error of the mean; 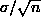
 The Central Limit Theorem
The Central Limit Theorem
 Tracking sample means and standard deviations: x-bar and s-charts. Setting control limits
Tracking sample means and standard deviations: x-bar and s-charts. Setting control limits
 Confidence intervals
Confidence intervals
 Using a confidence interval to make a decision
Using a confidence interval to make a decision
Standard error of the mean
 Sample means are less variable than raw data
Sample means are less variable than raw data
 SE(
SE( 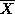 ) =
) = 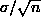 where
where  is the true s.d. of a single observation and n is the number of observations in the sample mean
is the true s.d. of a single observation and n is the number of observations in the sample mean
The Central Limit Theorem
 Sample means are approximately normally distributed. (see p.68 of CaseBook)
Sample means are approximately normally distributed. (see p.68 of CaseBook)
 E(
E( 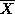 ) =
) = 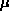 .
.
 Var(
Var( 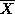 ) =
) = 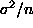 .
.
 s.d.(
s.d.( 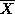 ) = SE(
) = SE( 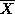 ) =
) = 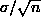 .
.
 Because sample means are approx. normal can use Empirical Rule on them.
Because sample means are approx. normal can use Empirical Rule on them.
Control charts
 Two types
Two types
 X-bar chart; track sample means
X-bar chart; track sample means
 s-chart; track sample standard deviations
s-chart; track sample standard deviations
 Setting the control limits - two ways (JMP gives choice);
Setting the control limits - two ways (JMP gives choice);
 From the engineer; use their specs to create limits
From the engineer; use their specs to create limits
 From the data; use overall sample mean and overall sample variance
plus the Empirical Rule to create limits (typically 3-sigma)
From the data; use overall sample mean and overall sample variance
plus the Empirical Rule to create limits (typically 3-sigma)
Two examples
 shaftxtr.jmp A well behaved process -- in control. p.70.
shaftxtr.jmp A well behaved process -- in control. p.70.
 carseam.jmp A process that fails to meet engineers specs. p.82.
carseam.jmp A process that fails to meet engineers specs. p.82.
Notes
 S-charts are usually one-sided in manufacturing
S-charts are usually one-sided in manufacturing
 Dealing with miracles; someone has to win the lottery but the same person should not win it three times in a row. Take action on observing a rare event.
Dealing with miracles; someone has to win the lottery but the same person should not win it three times in a row. Take action on observing a rare event.
 Daily means, weekly means, monthly means or WHAT? (p.80 of CaseBook) Better normality, less trawling and greater sensitivity (means pick up small changes faster -- up to a point).
Daily means, weekly means, monthly means or WHAT? (p.80 of CaseBook) Better normality, less trawling and greater sensitivity (means pick up small changes faster -- up to a point).
 Trawling through the data; the more things that are looked at the more likely we observe "false significance" (false positive - Type II error) pp.60,61 of CaseBook.
Trawling through the data; the more things that are looked at the more likely we observe "false significance" (false positive - Type II error) pp.60,61 of CaseBook.
Confidence intervals
 What is it?
What is it?
 1. A range of feasible values for an unknown population parameter, e.g.
1. A range of feasible values for an unknown population parameter, e.g. 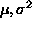 or
or 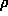
 2. A statement conveying the confidence that the range of feasible values really does include the unknown population value
2. A statement conveying the confidence that the range of feasible values really does include the unknown population value
 Where does it come from?
Where does it come from?
 Inverting the Empirical rule
Inverting the Empirical rule
 If 95% of the time the sample mean is within +/- 2 standard errors from
If 95% of the time the sample mean is within +/- 2 standard errors from 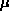 , then 95% of the time the true
, then 95% of the time the true 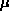 is within +/- 2 standard errors from the sample mean
is within +/- 2 standard errors from the sample mean
 Why is it important?
Why is it important?
 Move away from a single "estimate" to a range of values, which is more realistic
Move away from a single "estimate" to a range of values, which is more realistic
 Get to make the meta-level statement - our confidence
about the first statement
Get to make the meta-level statement - our confidence
about the first statement
 How do I use it to make a decision?
How do I use it to make a decision?
 Example, is 812 a feasible value for the true mean?
Example, is 812 a feasible value for the true mean?
 Answer: look to see if 812 lies in the confidence interval
Answer: look to see if 812 lies in the confidence interval
 If it's in the interval then it's a feasible value
If it's in the interval then it's a feasible value
 If it's outside the interval then it is not feasible
If it's outside the interval then it is not feasible
 shaftxtr.jmp A confidence interval for the population mean. p.99.
shaftxtr.jmp A confidence interval for the population mean. p.99.
 comppur.jmp A confidence interval for the intent to purchase. p.106.
comppur.jmp A confidence interval for the intent to purchase. p.106.
Richard Waterman
Sun Aug 10 14:54:13 EDT 1997
 shaftxtr.jmp A well behaved process -- in control. p.70.
shaftxtr.jmp A well behaved process -- in control. p.70.
 carseam.jmp A process that fails to meet engineers specs. p.82.
carseam.jmp A process that fails to meet engineers specs. p.82.
 shaftxtr.jmp A confidence interval for the population mean. p.99.
shaftxtr.jmp A confidence interval for the population mean. p.99.
 comppur.jmp A confidence interval for the intent to purchase. p.106.
comppur.jmp A confidence interval for the intent to purchase. p.106.