Class 4

What you need to know from last time

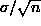The standard error of the sample mean; . It measures how accurate the sample mean is as an estimate of the population mean. No confusion - always use the formula (don't use the standard deviation of sample means)

The Central Limit Theorem

Tracking sample means and standard deviations: x-bar and s-charts. Setting control limits

Confidence intervals. For example, an approx 95% CI for 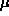is given by 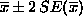. Can see how the standard error through the confidence interval conveys the accuracy of

Using a confidence interval to make a decision

Todays class - two themes

Sampling

Begin decision making - hypothesis testing

Sampling

Context; there is a target population - the group you wish to make inferences about. You draw a sample. Use the sample to make statements about the population.

Sample must be representative of the population

Sampling is the way to obtain reliable information in a cost effective way (why not census?)

Objective; collect information. Issues:

What to measure?

How accurate do we need it?

How often do we need it?

Does it meet end user requirements?

Issues in sampling

Representativeness

Interviewer discretion

Respondent discretion - non-response

Key question: is the reason for non-response related to the attribute you are trying to measure? Illegal aliens/Census. Start-up companies/not in phone book. Library exit survey.

Good samples;

Good samples; probability samples; each unit in the population has a known probability of being in the sample

Simplest case; equal probability sample, each unit has the same chance of being in the sample

Bad samples - the rest, convenience samples

The utopian sample for analysis

You have a complete and accurate list of ALL the units in the target population (sampling frame)

From this you draw an equal probability sample (generate a list of random numbers)

Reality check; incomplete frame, impossible frame, practical constraints on the simple random sample (cost and time of sampling)

Precision considerations

How large a sample do I need? p.117

Focus on confidence interval - choose coverage rate (90%, 95%, 99%) margin of error (half the width). Typically trade off width against coverage rate.

Simple rule of thumb for a population proportion - if it's a 95% CI then use n = 1/(margin of error)^2.

More issues

The independence assumption. No overlap of information between observations.

Finite population correction. What if population size is 400 and you sampled 399 of them?

Examples

survey1.jmp A hotel customer satisfaction survey.

survey2.jmp More on the survey.

Making decisions

Hypothesis testing

Deciding on one of two choices

Null hypothesis: status quo

Alternative hypothesis: the converse of the null

Example; jury trial. Null is Innocent. Alternative is Guilty

Note - one is taken as true a priori

Decision based on collecting data - the jury votes. If jury votes = 12 then convict else acquit and declare NOT GUILTY. Note, do not declare innocent!

Two types of error

Innocent, but declare guilty (null true but go with alternative - Type I)

Guilty, but say innocent (alternative true but go with null - Type II)

Price of the errors? Which is worse (think capital trial)

What should error rates be?

Beyond all reasonable doubt - very small chance of incorrectly declaring guilty - small chance of a Type I error

The preponderance of the evidence

Criminal vs. civil court - context, cost dependent.