Class 1 Stat 608

Simple Linear Regression

Plan.

Syllabus review

Simple Linear Regression (SLR) review

Setup

Interpretation

Assumptions and consequences

Checking assumptions

Prediction and confidence intervals

Graphics; scatterplot, residual plot, normal quantile plot.

The basics.

Setup, two variables. Y (response) and X (predictor)

Plan: fit a line through scatterplot of data (maybe transformed data)

The cardinal rule of data analysis: always, always plot your data.

Use this line (curve) for summarizing, predicting or explaining

The model: .

Interpretation of the coefficients in the model.

- the slope. For every one unit change in X, Y changes by .

- the intercept. The value of Y when X equals 0. May or may not make sense - depends on context.

If log transform (natural log) a variable the replace absolute change by percentage change (works for small percentage changes only, see p.23)

The "best line", minimizing the sum of vertical distances squared, the Least Squares Line.

Regression assumptions and how to check for them.

So far we have thought of our model as the rule that relates the average value of Y to X, that is .

The process that generates the data, the actual Y-variables themselves is often modeled as

That is we think of the data as coming from a two part process, a systematic part and a random part (signal plus noise). The noise part is sometimes due to measurement error and other times interpreted as all the important variables that should have been in the model but were left out.

The regression assumptions:

are independent.

are mean zero and have constant variance, and for all i.

are approximately normally distributed.

Consequences of violation of the assumptions:

If positive autocorrelation then we are over-optimistic about the information content in the data. We think that there is less noise than there really is. Confidence intervals too narrow.

Non-constant variance:

Incorrectly quantify the true uncertainty.

Prediction intervals are inaccurate.

Least squares is inefficient: if you understood the structure of better you could get better estimates of and .

If are symmetric then normality assumption is not a big deal. If are really skewed and you only have a small amount of data then it is all up the creek.

Since the assumptions are on the error term, the , we have to check them by looking at the "estimated errors", the residuals.

Note that is the distance from the point to the true line.

But the residual is the distance from the point to the estimated line.

Identifying unusual points; residuals, leverage and influence.

Points extreme in the X-direction are called points of high leverage.

Points extreme in the Y-direction are points with BIG residuals.

Points to watch out for are those that are high leverage and with a BIG residual. These are called influential points. Deleting them from the regression can change everything.

Page 63 is the key for outliers and leverage.

Understanding almost all the regression output

R-squared (correlation squared).

The proportion of variability in Y explained by the regression model.

Answers the question "how good is the fit"?

Root mean squared error (RMSE).

The spread of the points about the fitted model.

Answers the question "can you do good prediction"?

Write the variance of the as , then RMSE estimates .

Only a meaningful measure with respect to the range of Y (as it retains the scale of teh data).

A rule of thumb 95% prediction interval: up to the line +/- 2 RMSE (only works in the range of the data).

Confidence interval for the slope.

Answers the question "is there any point in it all"?

If the CI contains 0, then 0 is a feasible value for the slope, i.e. the line may be flat, that is X tells you nothing about Y.

The p-value associated with the slope is testing the hypothesis Slope = 0 vs Slope 0.

Two types of prediction (concentrate on the second)

Estimating an average, "where is the regression line"?

Range of feasible values should reflect uncertainty in the true regression line.

Predicting a new observation, "where's a new point going to be"?

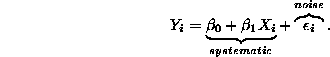
Range of feasible values should reflect uncertainty in the true regression line AND the variability of the points about the line.

What a difference a leveraged point can make (cottages.jmp).

   From pages 92 and 96.

     Measure      With outlier    Without outlier

     R-squared    0.78            0.075
     RMSE         3570             3634
     Slope        9.75             6.14
     SE(slope)    1.30             5.56

If someone comes with a great R-squared it does not mean they have a great model; maybe there is just a highly leveraged point well fit by the regression.

Examples

Cleaning.jmp p9,59.

Display.jmp p14,101.

Cottages.jmp p80

Direct.jmp p74

Phila.jmp p64