Class 3
What you need to have learnt from Class 2.

- What is multiple regression?

- The model:
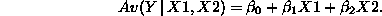

- The interpretation of the partial slopes in multiple
regression. Example: if we have two X variables X1 and X2 then the
partial slope of X1 is interpreted as "the change in Y for every
one unit change in X1 holding X2 constant".

- The essential difference between multiple regression and simple
(one X) regression - the fact that in multiple regression the X's
may be correlated which implies that looking at partial slopes or marginal
slopes can lead to different decisions.

- What makes a good model (it can depend on your
objectives).

- What can be learnt from a leverage plot.

- Collinearity.

- Correlation of the X's leads to an unstable regression plane.

- There is extreme uncertainty about the true slopes.

- This is not a problem if predicting in the range of the data.

- Know the consequences of collinearity.

- Understand the collinearity diagnostics.

- Be aware of the fix ups.

- Hypothesis testing - three types of test.

- Last in test - the t-test.

- ALL at once test - the ANOVA F-test.

- Testing a subset of variables - the Partial F-test.
Today's material
Including a categorical variable in a
regression.
Start with 2 groups in the categorical variable.
Key fact: When JMP compares two groups in a regression, the comparison
is between each group and the average of the two groups. In fact JMP
only compares one group to the average, but if you know that one group
is three below the average then you know that the other group must be
three above the average, so it's not a big deal.

- Parallel lines regression - allowing different intercepts for
the two groups.

- Declare the variable as NOMINAL.

- Add it just like any other X-variable.

- Including the categorical variable allows you to fit a separate
line to each group so that you can compare them.

- Recognize that the comparison is between each group and the
average of the two groups.

- Recognize that the lines are forced to be parallel.

- The "slope" estimate on the categorical variable is the
difference between one group and the average of the two groups for
the estimated Y-value.

- The height difference between the parallel lines is given by
twice the estimated slope for the categorical variable.

- Non-parallel lines regression - allowing different intercepts
and different slopes for each group.

- Declare the categorical variable as NOMINAL.

- Add it just like any other X-variable but also add the cross
product term. Cross product terms are sometimes known as
interaction terms.

- The "slope" on the categorical variable tells you the
difference between intercepts, comparing each group to the average
of the two groups.

- The "slope" on the cross product term tells you the
difference between slopes for the two groups, comparing each group
slope to the average of the group slopes.

-
An animation
explaining what exactly is going on in a categorical variable
regression.
Categorical variables with more than two groups.
Example consider three groups (G1,G2,G3).

- Parallel lines regression - Three of them, one for each group.

- Key fact: 3 groups, JMP gives 2 comparisons.

- G1 to average.

- G2 to average.

- You work out G3: if G1 is 4 above average and G2 is 3 above
average then G3 must be 7 below average.

- Rule: what number added to the others make them all sum to zero?

- A negative on a categorical variable coefficient say BELOW par.

- A positive on a categorical variable coefficient say ABOVE par.

- Non-parallel lines - 3 different intercepts and three
different slopes.

- Presenting categorical variable regression, an equation for
each group. Follows p.196 in the bulk pack.

-
Baseline: RunTime = 179.59 + 0.23 RunSize
G1 : RunTime = (179.5 + 22.94) + (0.23 + 0.07) Runsize
G2 : RunTime = (179.5 + 6.90) + (0.23 + -.10) Runsize
G3 : RunTime = (179.5 + -29.84) + (0.23 + -.03) Runsize

- Is a difference significant? Look at the t-stat.

- Are the differences significant? Look at a partial-F ("effect
test" in JMP).

- The partial-F
/ 2 2 \ /Number of
| R - R | / variables
\ BIG SMALL / / in the subset.
__________________________________________________________________
/ 2 \ / Number of observations
| 1 - R | / minus number of parameters
\ BIG / / in Big model. (inc. intercept).

- Strategy for when some groups are significantly different and
others are not: collapse the non-significant groups together.

- More than one categorical variable - fine. (e.g. gender and
race). What does a parallel lines regression mean here? Take Y
as income and explain it in English.

- Interaction with more than one variable (OK, three way interaction etc).
Examples
 Manager.jmp p163.
Manager.jmp p163.
 ProdTime.jmp p191.
ProdTime.jmp p191.
Richard Waterman
Tue Aug 19 14:43:25 EDT 1997

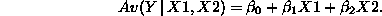
![]()
 Manager.jmp p163.
Manager.jmp p163.
 ProdTime.jmp p191.
ProdTime.jmp p191.