For next time read Berndt 3.5,3.6.
Todays class.
The game plan
- 1. Model learning curves
- 2. Model production functions
- 3. Model costs associated with production function
- 4. Specialize cost function to include the learning curve model
as a special case
1. Learning curves

- The motivation

- Unit costs decrease as cumulative output increases.

- Strategic implications for pricing and marketing strategy

- Formulation


where
-
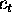 is unit cost in time period t (adjusted for inflation)
is unit cost in time period t (adjusted for inflation) -
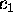 is unit cost in initial time period
is unit cost in initial time period -
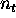 cumulative production up to but not including time t
cumulative production up to but not including time t -
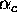 is unit cost elasticity with respect to cumulative volume
is unit cost elasticity with respect to cumulative volume -
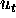 stochastic disturbance term (our
stochastic disturbance term (our 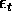 )
)

- Note. Response is unit cost. A multiplicative model.

- Make linear by taking logs.

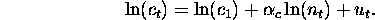

- Estimate
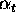 from a simple regression.
from a simple regression.
2. Cobb Douglas production function.

- Model:
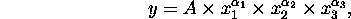
where
- y is the output
- A denotes the state of technical knowledge
-
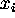 denotes the quantity of input i
denotes the quantity of input i -
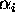 is the parameter to be estimated (like an elasticity of output with respect to input i)
is the parameter to be estimated (like an elasticity of output with respect to input i)

- Note: the response is output. Another multiplicative model.

- Define returns to scale as
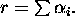
3. The cost function

- The cost function is
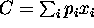 .
.

- Just the quantity of inputs times their prices.

- Relates the minimum cost of producing a level of output y to the
prices of the inputs and the state of technical knowledge.
Objective;
Find the input levels that minimze the production cost for a given
level of output. (Cost minimizer assumption.)
This is an optimization problem, in particular choose input levels to
minimize costs. But subject to a constraint: the inputs must produce a
given level of output, y.
Mathematical technique for solution of constrained optimization:
Lagrange multipliers.
It turns out that, assuming the Cobb Douglas production function, then
the optimal level of inputs produce a COST FUNCTION of the form
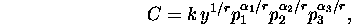
where
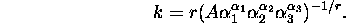
It looks a mess, but notice that it is multiplicative, so taking logs will
achieve a linear expression ready for regression.
Further, using the fact that 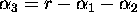 the logged
version can be rewritten as
the logged
version can be rewritten as
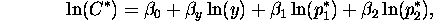
where
From this lot we can get at what's of interest, 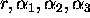 .
.
4. Putting together the Learning Curve and the Cost Function
Objective: make assumptions that incorporate the learning curve into the
cost function as a special case.
- Recall that the learning curve equation can be written as
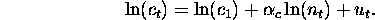
- And the cost equation as
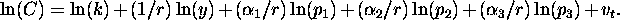
Then the question becomes can we put restrictions and assumptions on the
cost function so that the learning curve is a special case?
Here's how it goes.
- Define the state of knowledge
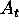 as
as 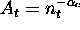 .
. - Assume that effects of the input prices are captured by a GNP deflator,
ie
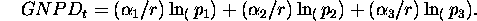
This leads to a simpler equation:
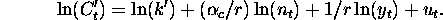
Here 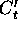 is a real total cost because it as been adjusted by the GNP
deflator.
is a real total cost because it as been adjusted by the GNP
deflator.
Finally move to unit real costs rather than total real costs and you obtain
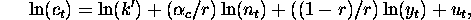
which for r = 1 is the learning curve model.
How much sense does the previous equation make?
It says that the log of your average real cost at time t depends on
two things.
- 1, how much you have produced up to time t which surrogates for
how much knowledge you have.
- 2, how much you produce at time t as denoted
by
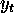 . If you produce more and your returns to scale are greater than 1
(r > 1) then your average cost should decrease - which makes sense.
. If you produce more and your returns to scale are greater than 1
(r > 1) then your average cost should decrease - which makes sense.
Summary
We have seen a variety of econometric models in action.
- There were all multiplicative.
- Their functional form was convenient to work with.
- They involved some very strong assumptions.
- Criticism should be tempered by the objective of the modeling.
- They provide a framework and language for discussion rather than a vague conversation.
Richard Waterman
Wed Oct 1 20:47:26 EDT 1997
![]()
![]()
![]()
![]()
![]()
![]() the logged
version can be rewritten as
the logged
version can be rewritten as
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]() is a real total cost because it as been adjusted by the GNP
deflator.
is a real total cost because it as been adjusted by the GNP
deflator.
![]()