Class 10 Stat701 Fall 1997

Fitting the Nerlove data.

Last time

Learning curves, production and cost functions.

Todays class.

Homework 1 comments

Three pronged attack in course

Exposure to useful models

Advanced analysis and methods

Implementation, Presentation and Communication

Review models - key points

Nerlove data and SPlus introduction

Key points from the econometric models

All multiplicative models - giving percentage change interpretations on the log scale.

Learning is proxied by the cumulative output.

Level of technology is also proxied by the cumulative output

Models have some obvious limitations - returns to scale does not depend on the level of X.

Can still value the models if you buy into them as approximations to a ``local'' reality.

Models manufactured to mirror economic theory.

A possible more hard-nosed approach. If your only objective is to predict cost, FORGET the theory, use and manipulate the explanatory variables in anyway that lets you do ``good'' prediction - closer to the Stat621 regression project view of the world.

Statistical points from Berndt

Underspecification - what's the impact of leaving out a variable that should be in the model?

What's the impact of fitting

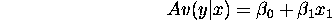
when the true model is

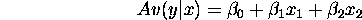
Answer: typically it biases the estimates of those that are left in - unless

The left out variable is uncorrelated with those that are in.

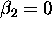
If you can design an experiment, it is often a good idea to build this feature in - make the X-s uncorrelated (aka orthogonal).

In the underspecified model RMSE is biased upwards - so you tend to be conservative - p.values too big, PI's too wide.

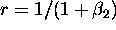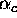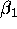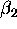Berndt on p.75 (3.35) recovers the returns to scale parameter r by using the relationship and likewise for . He then goes on to say that one cannot in general directly employ the estimated standard errors of and to compute confidence intervals for r and .

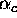However, there is a very computer intensive way of finding standard errors and confidence intervals for just about any ``smooth'' function of the original parameters. It is called the BOOTSTRAP.

Idea behind the bootstrap.

• Resample your data - take a random sample with replacement of rows from your spreadsheet.
• Recompute the regression and related statistics from this resampled dataset.
• Repeat many times, obtaining a bootstrap sample of parameter estimates.
• Estimate the standard error by calculating the standard deviation of the resampled estimates.
• Obtain bootstrap confidence intervals from the quantiles of the resampled estimates