Class 13 Stat701 Fall 1997

Weighted Least Squares and Monte Carlo Simulation.

Todays class.

• Heteroscedasticity and Weighted Least Squares.
• Monte Carlo studies.

Plan:

Review: unbiased and efficient.

Summarize Ordinary Least squares under heteroscedasticity.

Consider options and their properties.

Discuss Monte Carlo simulations.

Look at simulation results.

Data analysis example -- housing prices and pollution.

What makes a good estimate?

A good estimator, 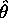of a population parameter 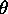has at least two properties:

On average it takes on the correct value, that is 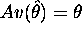: UNBIASED

It is most concentrated around the true value: EFFICIENT

Monte Carlo studies.

A stochastic extension of scenario analysis.

Best case scenario

Typical case scenario

Worst case scenario

Problem: they are not equally likely to happen

Would like to include in the overall evaluation the probability/frequency that each scenario happens.

Monte Carlo refinement: let the computer randomly generate the scenarios (many of them - hopefully with frequencies in accordance with reality) and evaluate strategies over these random draws.

Generate a world - evaluate an action on that world.

Potentially much more informative - for example can talk about the ``chances'' that an event happens.

Downside - if computer generates incongruent scenarios then get garbage.

Very effective when mechanism to generate world is simple but evaluating an action in that world is complex, e.g. simple models for the market (the world) but need to price a complex derivative (the action)

The foundation for the analysis: the Law of Large Numbers (maybe the colloquial law of averages)

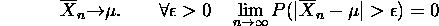
Apply to indicators of an event happening: then in English proportion of times that an event happens in the simulation tends to the probability that the event happens.

Simulation results.

Housing data example.

Check: Does the statement
the long run probability that it rains tomorrow is 0.3
confuse you.

It shouldn't: the term long run has nothing to do with way into the future. It just means averaging over an increasing number of events.