Class 19 Stat701 Fall 1997

Introduction to Neural Networks

Todays class.

Classification in the internet demographics dataset.

Introduction to Neural Nets.

Discussion points from the Lo paper on Neural Nets.

Installing the nnet library.
key SPlus command library(nnet,first=T,lib.loc=''C:/public'')

Neural nets in action for classification - an example for which the true classification probabilities are known

NNet classification example on the internet demographics data set.

Adding gold to the data - does the net find it?

A pre-prepared page of graphics - just in case we bomb in class

Classification in the internet demographics dataset.

Building classification models.
Judging models on out of sample prediction.

Introduction to Neural Nets.

We will consider the Feedforward Perceptron with a Single Hidden Layer.

It's objective is to output probabilities of group membership based on a set of inputs.

Figure 1 is a diagram of a single hidden layer network. Essentially it links inputs to outputs through a set of weights and activation functions. In class we will only use the ``logistic'' activation function though others are available. In the displayed network there are two inputs and three units in the hidden layer.

Therefore between the input layer and the hidden layer we are looking for the following weights

Link X1 and X2 to H1. Weights g11 and g12.
Link X1 and X2 to H2. Weights g21 and g22.
Link X1 and X2 to H3. Weights g31 and g32.

Now apply the activation function T (logistic) to each hidden unit to get

T(g11 X1 + g12 X2)
T(g21 X1 + g22 X2)
T(g31 X1 + g32 X2)

The procedure also looks for weights d1, d2 and d3 to form

d1 T(g11 X1 + g12 X2) + d2 T(g21 X1 + g22 X2) + T(g31 X1 + g32 X2),

and finally the output is given by

T(d1 T(g11 X1 + g12 X2) + d2 T(g21 X1 + g22 X2) + T(g31 X1 + g32 X2))

Figure 1.

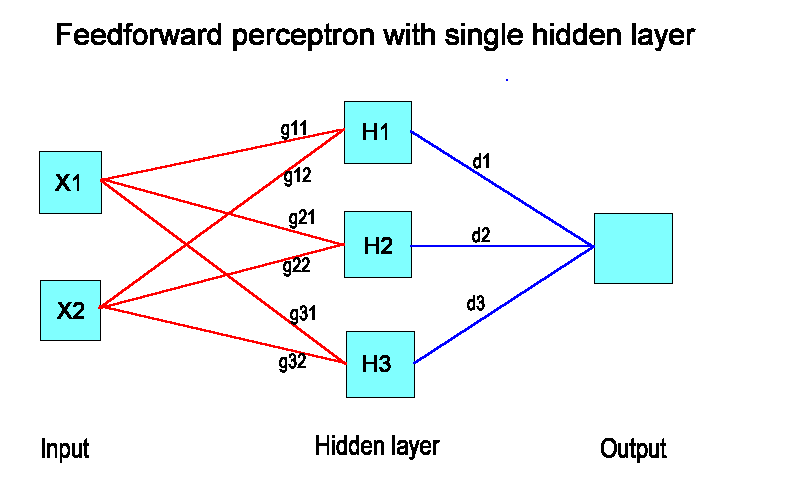
Fitting a given net involves finding the set of weights that best matches observed and predicted outputs.

It is the inclusion of the hidden layer that makes the network a very flexible fitting tool.

Compare the neural network diagram to the previous logistic regression diagram.

Discussion points from the Lo paper on Neural Nets.

• It is a non-parametric technique. Does not assume an explicit functional form for the relationship between inputs and outputs.
• This is useful for capturing possible non-linearities in the relationship.
• The nets relate inputs to outputs through weights and activation functions
• A hidden layer enables them to be extremely flexible - universal approximators
• Downside - if the network can fit anything - it can fit the noise as well as the signal
• Do they learn? What does ``learn'' mean anyway. Weights change if data is updated.
• Standard statistical inference on the model parameters (weights) is not readily available.
• But inference is not such a big deal if sole objective is prediction and out of sample validation is followed.
• Models are not generally well defined, small changes in the data can lead to large changes in weights
• Weights are not interpretable in the sense that regression weights (partial slopes) are.
• The objective function (the object that is maximized to choose the weights) may have local maxima. Practical solution - set algorithm off at different starting values.
• It is one of many non-parametric techniques - similar in this sense to splines and kernel methods.
• Practically, may need much human supervision if they are to produce coherent results - as with many technologies, they do new things but require more work.
• A useful additional member of the quantitative tool box - but no panacea, probably more dangerous than regression in the wrong hands!