Class 24 Stat701 Fall 1997
RiskMetrics
Todays class.

- Homework comments|Due date|code|

- Homework (part 2):
Time series question. Background reading
Berndt.
6.1 Introduction
6.6 Time series model
6.7B MA motivation
Exercise 7, p. 289

- Resources: RiskMetrics Readings and links.

- VAR, RiskMetrics and Market Risk Methodology.
Jacques Longerstaey.
Capital Market Strategies, July 1995. Provides motivation and context for
the methodology - compares with standard methods.

-
 #95-19.
#95-19.
Probability and Statistics Applied to the Practice
of Financial Risk Management: The Case of JP Morgan's RiskMetrics
Michael Phelan, August 1995.
A distillation of the technical aspects from a statistics and
probability perspective.

-
RiskMetrics
Documentation from the horses mouth.
More documentation.
Issues to consider when reading the Longerstaey paper.
- A wider context
- Stochastic component: recognition of uncertainty and the requirement to
quantify this uncertainty.
- Improved data processing skills/power.
- Techniques: basic measures mean, s.d./variance, correlation.
- Linearity assumptions.
- Normal distributions, joint movements/distributions.
- Probability statements for describing uncertainty:
- Parametrically based -- percentiles from the normal distribution..
- Non-parametrically based -- empirical percentiles.
- The creation of virtual worlds;
- Assumption based vs. history based.
- Taylor's theorem/series. Locally the world is linear.
- The delta method - not delta hedging but still about linearity!
- Quantify the lack of linearity - curvature corrections.
Forecasts.
Exponential smoothing.
The method described here is for non-seasonal time
series showing no systematic trend.
Data: 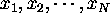 .
.
Define the 1 step ahead forecast from N points as 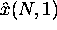 , then
, then
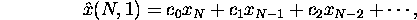
where the 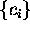 are weights.
are weights.
Downweight points further back in time.
Use Geometric weights: 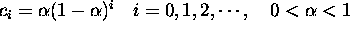 .
.
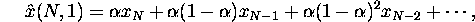
needs an infinite number of observations, but realistically only have
a finite number.
Write in recurrence form:
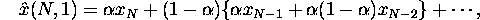
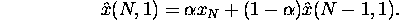
Update using the last observation and last forecast.
It's a weighted average between observed and expected
at time N.
Or can express in error correction form;
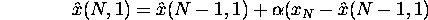
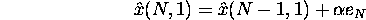
It turns out that exponential smoothing is ``optimal'' if the underlying
process is
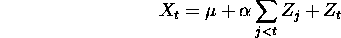
which gives the differenced series as MA(1), so that 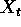 is ARIMA(0,1,1).
In particular
is ARIMA(0,1,1).
In particular
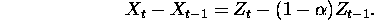
Richard Waterman
Mon Dec 1 20:36:32 EST 1997


 #95-19.
#95-19.
