Class 3. Stat701 Fall 1998

Recap

• Last time we reviewed the simple linear regression model.
• Normal quantile plots were discussed.

Volatility model

We consider a simple model that would give rise to two volatility regimes on returns.

The volatility regime model, in which trades take place at different rates over the course of a day, relies on knowing the key facts that

The sum of normal random variables is again normal

The variance of a sum is the sum of the variances when the observations are independent

The return over a fixed period (say a day) is approximately equal to the sum of returns over contained shorter periods (say hours)

Example:

Comparing hourly returns and the daily return.

HOUR	0	1	2	3	4	5	6	7
Value	100.0000	99.4819	99.6610	100.6495	101.5622	102.7503	100.9752	101.2928
Hourly return	***	-0.0052	0.0018	0.0099	0.0091	0.0117	-0.0173	0.0031

Daily return = 0.0129.
Sum of hourly returns = 0.0131

The sum of the hourly returns approximates the daily return.

If the hourly returns are approximately normal, then so is their sum, but this is just the daily return. The daily return is a sum, and the variance of a sum is the sum of the variances (provided the returns are independent), so if you buy into the model then daily returns have more variance than the hourly returns.

Todays material: looking at categorical variables.

Parallel lines regression.

Interaction terms in categorical variables.

Interaction: a three variable concept. One Y and two X's. X1 and X2.

The impact of X1 on Y depends on the level of X2.

In the gold example; the impact of SP500 return on gold return depends on the date (Pre 1980 vs. Post 1980).

In formulae, denote the categorical variable by z, and let z = 1 for group 1 and z = -1 for group 2. Then for group 1:

and group 2

Hence is the difference in intercepts and is the difference in slopes.

When doing categorical variable regression always check the residuals for each group.

Comparison boxplots are good for this.

What you need to know:

The basic graphics for simple regression

The interpretation of the regression coefficients

The interpretation of the number summaries, 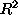, RMSE.

Inference: confidence intervals for the slope, p-values

Next time

Start multiple regression. This is chapter 3 in Berndt.

We will use this to review transformation, prediction and categorical variables with more than two groups.