Logistic regression to Neural Nets.

Further discussion of classification

Todays class.

Two readings to be distributed next time with discussion:
Data snooping in financial analysis. Andrew Lo.
Neural networks and other non-parametric techniques in economics and finance. Andrew Lo.

Key point from last time: Always check forecasting error OUT OF SAMPLE

A nueral-net perspective on logistic regression

Logistic regression

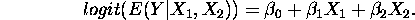
or

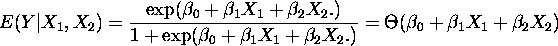
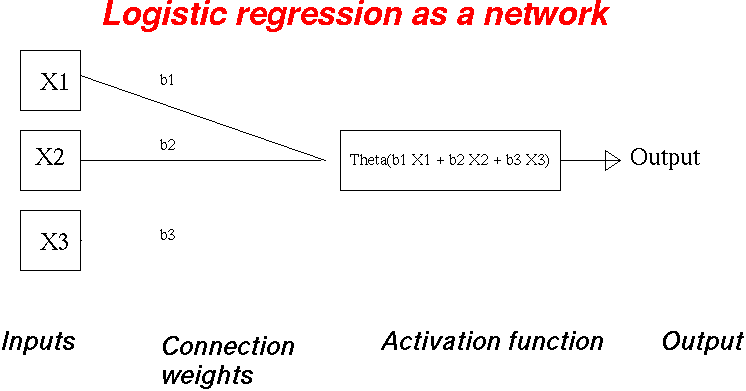
Single layer feed forward perceptron.

Inputs:

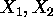
Target variable:

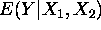
Connection weights:

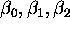
activation function:

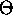
In English what you do;

Weight the inputs

Sum them

Apply the activation function to them.

Choosing the weights: as ever, chosen to minimise or maximize an objective function. Minimize errors - maximize closeness of observed and fitted values.

• Squared error
• Entropy
• Likeliood

At the end of the fitting exercise we have the weights, that can be applied to a new observation to do prediction.

Further, if we get more data, we can re-estimate the weights - then the machine is ``learning''.

How many inputs?

This is a model fitting exercise and contains all the usual subtelties.

Classification

Recall that we will classify an observation as a ``1'' if the estimated probability that Y equals 1 is greater than 0.5.

This is entirely equivalent to the logit of the probability being greater than 0.

If we had a simple two variable model with say X1 and X2, then we classify as a ``1'' if .

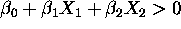To be specific, say 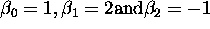, then when does the logistic regression classify as a one?

Answer: whenever .

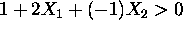In X1, X2 space this is:

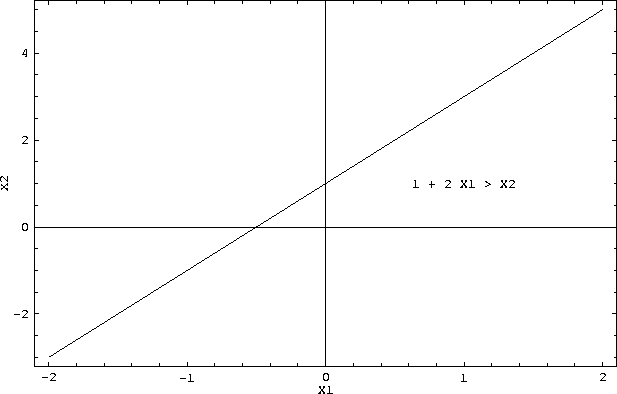
So, the classifier splits the X1 , X2 space into two pieces.

But what if the distribution of 0's and 1's in the X1, X2 space is much more complex, say it looked like this

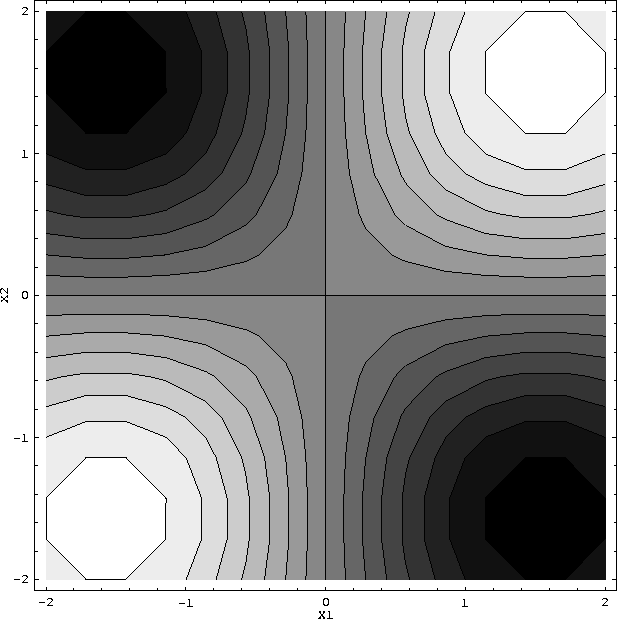
This is where Neural nets come in.