Stat701 Fall 1998

Time series: models and forecasts.

References:
Chris Chatfield. The Analysis of Time Series.Chapman and Hall.

Todays class.

*
Introduction.
*
Descriptive techniques.
*
Series with trend - linear filters
*
Autocorrelation
*
The correlogram
*
Processes
*
A purely random process
*
A random walk
*
Moving average process (MA)
*
Autoregressive process (AR)
*
Mixed ARMA models

*
Types of series
*
Economic series: interest rate
*
Physical series: temperature
*
Marketing series: sales
*
Demographic: population series
*
Process control: yield

*
Objectives in time series analysis
*
Description
*
Explanation
*
Prediction
*
Control

*
Overall plan: descriptive techniques, probability models, fitting the models, forecasting procedures
*
Analysis in the time domain not the frequency domain (see stat 711 for this).

Types of variation: extracting the main properties in a series.

*
Seasonal effect - measure and/or remove
*
Other cyclic changes
*
Trend - long term change in the mean level
*
Other irregular fluctuations - the residuals, can they be explained via models such as moving average or autoregressive.
*
Stationary time series - no systematic change in the mean or the variance and no strictly periodic variations. Most theory is concerned with stationary time series - so need this assumption to use theory.
*
The time plot: plotting the series against time - picks up important features such as trend, seasonality, outliers and discontinuities

Analyzing series that contain a trend

*
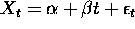
Model it: tex2html_wrap_inline167
*
Filter it
*
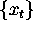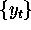Turn one time series tex2html_wrap_inline169 into another tex2html_wrap_inline171 by a linear operation

displaymath173

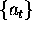where tex2html_wrap_inline175 is a set of weights.

*
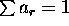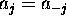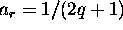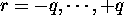To smooth out fluctuations and estimate the local mean set tex2html_wrap_inline177 - the moving average. Often symmetric with s = q and tex2html_wrap_inline181 . The simple moving average: a symmetric smoothing filter with tex2html_wrap_inline183 for tex2html_wrap_inline185 .
*
Can also choose weights to fit a local polynomial - very close to splines.
*
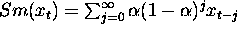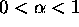Exponential smoothing: tex2html_wrap_inline187 , where tex2html_wrap_inline189 .
*
What sort of filter? To see the trend need to remove local fluctuations, the high frequency variation - therefore need a low-pass filter.
*
To see residuals remove low frequency variation - want a high-pass filter.
*
A very familiar filter 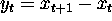tex2html_wrap_inline191 , differencing. For non-seasonal data this may be enough to obtain near stationarity.

Series with seasonal variation

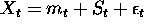A simple additive model: tex2html_wrap_inline193 .

To estimate the seasonal effect for a particular period, find the average for that period minus the corresponding yearly average.

To remove a seasonal effect with monthly data use the filter

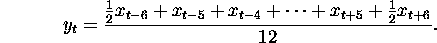
displaymath196

To remove a seasonal effect with quarterly data use the filter

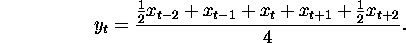
displaymath198

Autocorrelation

Measures of the correlation at different distances apart in time.

Lag 1 autocorrelation measures the correlation between observations 1 time unit apart.

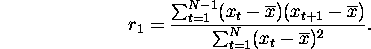
displaymath199

Lag k autocorrelation:

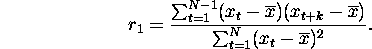
displaymath201

The correlogram: a plot of 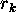tex2html_wrap_inline203 against k.

Interpretation of the correlogram:

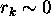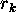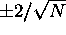
If time series is completely random then for large N, tex2html_wrap_inline205 . In fact tex2html_wrap_inline203 is approx N(0,1/N), so estimates should typically be within tex2html_wrap_inline210

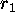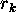Short term correlation. Stationary series often have a fairly large tex2html_wrap_inline211 , a few coefficients greater than 0 but getting successively smaller, and for large k, tex2html_wrap_inline203 is about 0.

Alternating series: Successive observations alternating on different sides of the overall mean, the correlogram alternates too.

Non-stationary series with a trend: 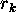tex2html_wrap_inline203 comes down slowly. In fact 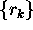tex2html_wrap_inline217 is only meaningful for stationary series - detrend first.

Seasonal fluctuations: if time series has a seasonal fluctuation then correlogram has fluctuation at the same frequency.


Richard Waterman