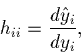Next: 2.2
Up: 2.
Previous: 2.
The plain residual ei and its plot is useful for checking how well the
regression line fits the data, and in particular if there is any systematic
lack of fit, for example curvature.
But, what value should be considered as a big residual?

- Problem: ei retains the scale of the response variable (Y).

- Answer: standardize by an estimate of the variance of the residual.

- Know,
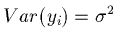 estimated by (RMSE)2.
estimated by (RMSE)2.

- But,
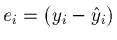 ,
which is more than just yi.
,
which is more than just yi.

- Turns out,
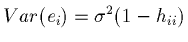 .
.

- Use standardized residual, si.

- The quantity, hii is fundamental to regression.

- An heuristic explanation of hii (visually we are dragging a
single point upward and measuring how the regression line follows):

- Think about yi the observed value,
and
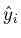 the
estimated value (ie the point on the regression line).
the
estimated value (ie the point on the regression line).

- For a fixed xi perturb yi a little bit,
how much do you expect
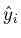 to move?
to move?

- If
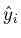 moves as much as yi then clearly yi has the
potential to drive the regression - so yi is leveraged.
moves as much as yi then clearly yi has the
potential to drive the regression - so yi is leveraged.

- If
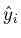 hardly moves at all then clearly yi has
no chance of driving the regression.
hardly moves at all then clearly yi has
no chance of driving the regression.

- In other words hii is the measure of ``leverage''.

- More precisely
and it depends only on the x-values.

- Understanding leverage is essential in regression because leverage
exposes the potential role of individual data points. Do you want your
decision to be based on a single observation?



Next: 2.2
Up: 2.
Previous: 2.
Richard Waterman
1999-09-20

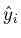 the
estimated value (ie the point on the regression line).
the
estimated value (ie the point on the regression line).

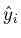 to move?
to move?

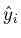 moves as much as yi then clearly yi has the
potential to drive the regression - so yi is leveraged.
moves as much as yi then clearly yi has the
potential to drive the regression - so yi is leveraged.

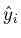 hardly moves at all then clearly yi has
no chance of driving the regression.
hardly moves at all then clearly yi has
no chance of driving the regression.