Class 9. Bootstrap Examples.

Bootstrap objective: measure the precision of the summary of interest.

Step 1. Start with a data set and a summary of interest, $\hat\theta$, say a trimmed mean (remove largest and smallest observation then find the mean).

$$\left[ \begin{array}{c} 3 \\ 5 \\ 4 \\ 6 \\ 1 \\ \hat\theta = 4 \\ \end{array}\right].$$

Step 2. Generate a set of virtual spreadsheets by randomly sampling row of the original spreadsheet, (B of them) by SRSWR. We'll find B = 4 bootstrap replicates.

Random rows, generated by computer, are (1,5,1,4,1), (1,3,1,2,4), (4,1,5,5,4), (4,2,4,3,1), giving spreadsheets:

$$\left[ \begin{array}{c} 3 \\ 1 \\ 3 \\ 6 \\ 3 \\ \hat\th... ... \\ 6 \\ 4 \\ 3 \\ \hat\theta_4 = 5 \\ \end{array}\right]$$

This gives 4 bootstrap estimates of $\theta$, $\theta_i$, 3, 4, 3.333 and 5.

Step 3. Find the sample standard deviation, s_B, of these bootstrap estimates.

$$s_B = \sqrt{\frac{\sum_{j = 1}^B(\hat\theta_j - \overline{\hat\theta})^2} {B - 1}},$$

where $\overline{\hat\theta}$ is the sample average of the bootstrap estimates.

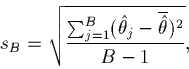
In this particular case s_b = 0.88. Use $\hat\theta \pm 2 \, s_B$ as an approximate 95% confidence interval for the parameter.

How large a B do I need. Rules of thumb: between 200 -2000.