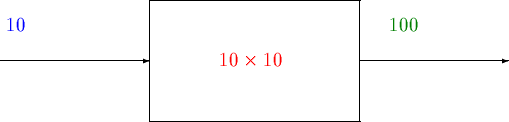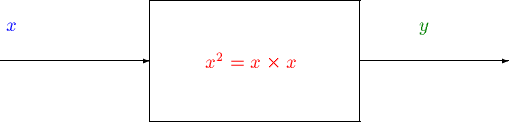
So far, the three functions we have looked at have all been linear functions (the constant and multiplicative functions are special cases of a linear function - the constant function is a linear function where the multiplicative factor is zero, and the multiplicative function is a linear function in which the constant is zero).
Linear functions are fundamental to all applied mathematics. They are the sole subject of Class2 in this series. However, they are not the only functions. Functions which are not linear, are not surprisingly called non-linear.
An example of a non-linear function is the square function whose rule is: multiply the input by itself.
It can be represented as
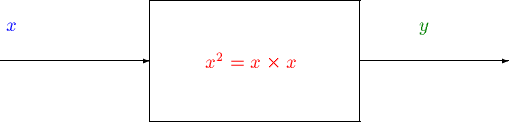
An example: