Many processes in life tend to be a bit more complicated than a single input and a single output - in particular one process often leads into another. Or put another way, sometimes it is a good idea to break a complex process down into a series of simpler ones. A key problem solving skill is to be able to take a complex problem and break it down into a sequence of simpler ones.
As an example of processes leading into another take an
an organization which has 250 employees, and in which
each employee works 8 hours a day. Assume that the hourly wage
rate is 20$/hour. In order to calculate the total labor costs
per day a two step procedure is needed:
first calculate the total employee hours per day. This is
represented by the function y=f(x), where y is the total
number of employee hours per day, x is the number of employees
and f is the rule ``multiply by 8'', that is
![]()
In particular:
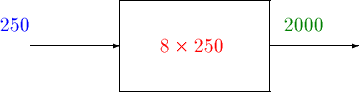
Now, as the wage rate is $20/hour, if we take the employee hours per day and multiply by 20 we get the total labor cost per day. This can be represented as z = g(y), where z is the total labor cost per day, y is the total employee hours per day, and g is the rule ``multiply by 20''.
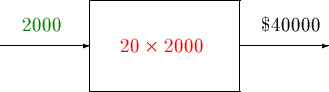
We could in fact combine the above two rules into a single representation:

Written Mathematically, we have

This is written symbolically as z = g(y) = g(f(x)). It is called a composition of functions.
The value of this representation, is, as stated earlier that good problem solving often involves breaking complex problems into a chain of simpler ones. Later in the course, we will study particular techniques for analyzing these compositions (or chains) of functions.