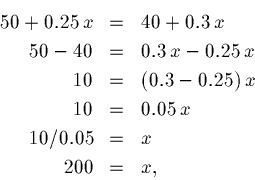3.4.2 Two lines

At this stage let's introduce another manager. Call the first manager, A, and this new manager, B.

Manager B takes a shorter time, 40 hours, to set up the production line, but then takes 18 minutes to produce each unit.

First, translate this statement into a production line function:

$$\fbox{$y = 40 + 0.3 \,x.$ }$$

We can plot both functions on the same graph.

Questions:

Who does a 50 unit job the quickest?

Generic: for a given value of x which line has the smaller value of y?

This can be done 2 ways, graphically, by just drawing a vertical line at x = 50, or by plugging in the number 50 to both production time equations and looking to see which manager takes the shorter time. So the answer is Manager B.

For which run size, is it irrelevant from a time perspective, which manager gets it?

Generic: where do the 2 lines cross?

This is an important question and arises in a variety of areas, particularly in the section on optimization:

The key realization is that where the lines cross, both the x-values and y-values for each manager must be identical (that's the definition of crossing).

We have an equation for each manager

$$\begin{eqnarray*}\mbox{\rm Manager 1:} \qquad y &=& 50 + 0.25 \,x \\ \mbox{\rm Manager 2:} \qquad y &=& 40 + 0.3 \,x \end{eqnarray*}$$

and since the left hand sides (LHS) must be equal at the crossing point, we can relate the two right hand-sides (RHS).

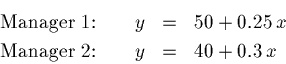
Equating the 2 right hand sides and doing the algebra then indicates:

$$\begin{eqnarray*}50 + 0.25\,x &=& 40 + 0.3\,x\\ 50 - 40 &=& 0.3\,x - 0.25\,x\\ ... ...(0.3 - 0.25) \,x\\ 10 &=& 0.05\,x\\ 10/0.05&=& x\\ 200 &=& x, \end{eqnarray*}$$

so that it is a 200 item job that takes both managers an identical amount of time.