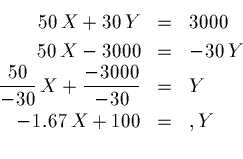4.1 Identifying the constraints

Call X the number of Type A networks installed.

Call Y the number of Type B networks involved,

Then the labor constraint on skilled labor implies that

$$\fbox{$10\,X + 40\,Y \le 800$ ,}$$

because we couldn't for example install 100 Type A networks, because that would require 1000 skilled labor hours and there are only have 800 available.

The labor constraint on semi-skilled labor indicates that

$$\fbox{$50\,X + 30\,Y \le 3000$ .}$$

Also, X and Y need to be greater than or equal to zero, as you can't install a negative number of networks!

We proceed by graphing the skilled labor constraint. First consider special case where $10\,X + 40\,Y = 800$. This statement can be rearranged as follows,

$$\begin{eqnarray*}10\,X + 40\,Y &=& 800 \\ 10\,X -800 &=& -40\,Y \\ \frac{10}{-40}\,X + \frac{-800}{-40} &=& Y \\ -0.25\,X + 20 &=& Y \\ \end{eqnarray*}$$

which re-expresses the relationship in the familiar straight line form, which can then be graphed as usual.

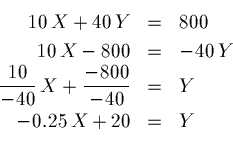
A quick way to do this is to, recognize the equation as that of a line, know that 2 points define a line, work out 2 points on the line, in particular these 2 easy cases will do: if X = 0, then Y = 20 and if Y=0 then X = 80.

This graph shows the feasible region for the skilled labor constraint.

Now for the semi-skilled labor requirements: $50\,X + 30\,Y \le 3000$.

$$\begin{eqnarray*}50\,X + 30\,Y &=& 3000 \\ 50\,X -3000 &=& -30\,Y \\ \frac{50}{-30}\,X + \frac{-3000}{-30} &=& Y \\ -1.67\,X + 100 &=& ,Y \\ \end{eqnarray*}$$

which when plotted identifies the feasible region as displayed in this graph.