4.4 Identifying the optimal network combination

The best solution is found where the two constraint lines cross.

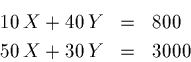
Another technique for finding where the lines cross, is to adjust one equation, so that you can reduce the 2 equations in 2 unknowns, to a single equation in one unknown.

Start with the 2 equations to solve

$$\begin{eqnarray*}10\,X + 40\,Y &=& 800 \\ 50\,X + 30\,Y &=& 3000 \end{eqnarray*}$$

Multiply both sides of the first equation by 5, to get

$$\begin{eqnarray*}50\,X + 200\,Y &=& 4000 \\ 50\,X + 30\,Y &=& 3000 \end{eqnarray*}$$

Take the second equations away from the first to get

$$170\,Y = 1000,$$

or Y = 5.88.

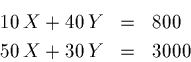
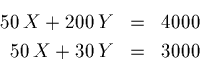
Substituting this value of Y back into the first equation, $10\,X + 40\,Y = 800$, gives:

$$\begin{eqnarray*}50\,X + 200\times 5.88 &=& 4000 \\ 50\,X +1176.47 &=& 4000 \\ 50\,X &=& 2823.53 \\ X &=& 56.47 \end{eqnarray*}$$

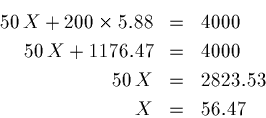
So the solution is (X = 56.47, Y = 5.88). Rounding these numbers (as we can't install fractional networks) gives 56 Type A networks and 6 Type B networks, indicating that the profit will be $56 \times 1000 + 6 \times 1200 = 63200$.