5.5 Logs base e

A special base for logs is the log base e. Written as ln.

ln(x) = log_e(x).

So

ln(e^x) = log_e(e^x) = x.

Taking natural logs undoes ``e'' to the power ...

A very useful interpretative fact to be explained later:

For small values of h

$$\fbox{$ln(1 + h) \sim h.$ }$$

For example ln (1.01) is about equal to 0.01, (in fact 0.009950331).

Say we have increases of sales from time 0 to time 1, of 1%. That is 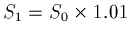$S_1 = S_0 \times 1.01$. So

$$ln(S_1) = ln(S_0 \times 1.01) = ln(S_0) + ln(1.01) = ln(S_0) + ln(1 + 0.01) \sim ln(S_0) + 0.01.$$

Therefore the difference in logs:

ln(S₁) - ln(S₀) = ln(S₀) + 0.01 - ln(S₀) = 0.01.

So the difference in logs gets interpreted as a ``percent change'' for small changes.