4.2 Calculating terms in a geometric series

Example: a customer satisfaction survey.

50000 past customers.

Telephone survey: 5% of those called reached on each phase - 95% not reached.

How many phases needed until 20% are reached? (NOT 4!).

Application: time line; project planning, the how long question.

During the first phase how many out of 50000 are reached? $0.05 \times 50000 = 2500$.

 

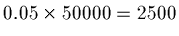Table 2: Number of customers not reached, reached and cumulative reach at the end of each phase.

Phase	Called	Unreached.	Reached	Cumulative reached
0	0	50,000	0	0
1	50,000	47,500	2500	2500
2	47,500	45,125	2375	4875
3	45,125	42,869	2256	7131
4	42,869	40,725	2143	9275
5	40,725	38,689	2036	11311

How many phases needed until 20% are reached? Answer: 5 phases.

How many not reached at phase t? Answer is $50,000 \times 0.95^t$.

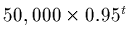This is an example of a mathematical model.

Rule: if the number is less than 1, the higher the power that you raise it to, the smaller the result - basic model reality check - yes, the number unreached decreases.

Again, it is a geometric series. Start with a quantity, (50,000), and repeatedly subject it to a constant proportionate change (0.95).

Question: what value of t (how long) until 20% are reached - that's 80% not reached.

$$\fbox{$50000 \times 0.95^t \le 40000.$ }$$

Solve the equality:

$$\fbox{$50000 \times 0.95^t = 40000.$ }$$

If you are solving for a ``power'' take logs. Objective: isolate t.

$$\begin{eqnarray*}50000 \times 0.95^t &=& 40000, \\ 0.95^t &=& \frac{40000}{500... ...0.2231 \\ t &=& \frac{-0.2231}{-0.05129} \\ t &=& 4.401 \\ \end{eqnarray*}$$

Answer: either 4 or 5 phases. What to do with this t? Options:

Try 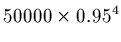$50000 \times 0.95^4$ (not enough), and 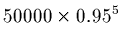$50000 \times 0.95^5$ (enough).

Look back in table.

Remember: if the number is less than 1, the higher the power that you raise it to, the smaller the result.

You do one, how many phases until at least half the customers are reached ?