4.4 ** Derivation of the sum

Summation notation introduction.

$$S_t = \sum_{i=0}^t P_0 \theta^i = P_0 \sum_{i=0}^t \theta^i.$$

$$S_t = P_0 \sum_{i=0}^t \theta^i.$$

How to find out what S_t is?

$$\begin{eqnarray*}S_t &=& P_0 \left(1 + \theta^1 + \theta^2 + \theta^3 + \cdots +... ... \\ S_t &=& P_0 \frac{(1 - \theta^{t + 1})}{1 - \theta}. \\ \end{eqnarray*}$$

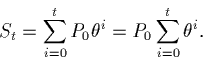
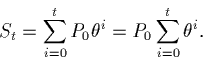
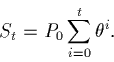
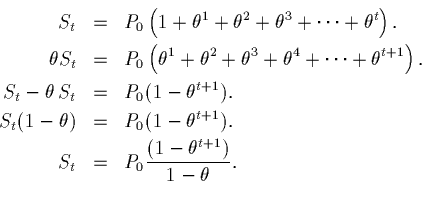
Always check this sort of formula with an example calculation:

Take P₀ = 1, $\theta = 0.5$ and t = 3.

Then

$$1 \times (\theta^0 + \theta^1 + \theta^2 + \theta^3)$$

0.5⁰ + 0.5¹ + 0.5² + 0.5³

1 + 0.5 + 0.25 + 0.125 = 1.875

The formula gives

$$1 \times \frac{(1 - 0.5^4)}{1 - 0.5} = \frac{1 - 0.0625}{1 - 0.5} = 1.875.$$

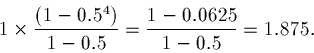
Recall the formula for the sum of the first t+1 terms is

$$S_t = P_0 \frac{(1 - \theta^{t + 1})}{1 - \theta}.$$

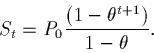
What about the limit of this series as $t \rightarrow \infty$?

Answer is that it depends on the magnitude of $\theta$, converges for $\theta < 1$.