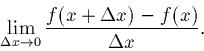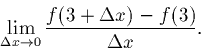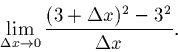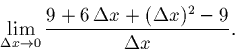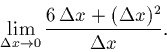Next: 4.2
Up: 4.
Previous: 4.
This section introduces the derivative. Recall derivative measures change,
change is what is of interest, so we are measuring what is of interest!
Here's a sketch of how we will get to the derivative:

- Draw a picture of the secant line approximation
to a function at a particular point (x).

- The tangent line
is the limit of the secant line as the "interval" (
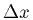 )
gets smaller.
)
gets smaller.

- The derivative is the slope of the tangent line at x.

- The derivative
of a function at the point x is defined as
In English, the derivative is the "rate of change" of the function.
Take a look at these ideas
pictorially:
As 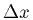 gets smaller and smaller, how much does y change, and what
about the slope, that is the ratio of
gets smaller and smaller, how much does y change, and what
about the slope, that is the ratio of
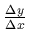 ?
?
Table 1:
Calculation of the slope of the secant line approximation to the
function y = x2 about the point x = 3.
| x |
y = x2 |
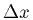 |
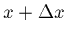 |
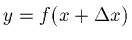 |
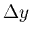 |
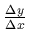 |
| 3 |
9 |
4 |
7 |
49 |
40 |
10 |
| 3 |
9 |
3 |
6 |
36 |
27 |
9 |
| 3 |
9 |
2 |
5 |
25 |
16 |
8 |
| 3 |
9 |
1 |
4 |
16 |
7 |
7 |
| 3.00 |
9.00 |
0.50 |
3.50 |
12.25 |
3.25 |
6.50 |
| 3.0000 |
9.0000 |
0.2500 |
3.2500 |
10.5625 |
1.5625 |
6.2500 |
| 3.00 |
9.00 |
0.10 |
3.10 |
9.61 |
0.61 |
6.10 |
| 3.0000 |
9.0000 |
0.0100 |
3.0100 |
9.0601 |
0.0601 |
6.0100 |
|
Note, that the ratio tends to a limit!
Call this limit,
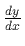 .
Note the lower case
d's rather than the
.
Note the lower case
d's rather than the  's.
's.
Formally defined as
Do an example (once) ...
Take the function, f, where
f(x) = x2.
'
So, the answer is 6, just as the picture suggested.
Back to interpretation.
Consider a function that tells you how far you have gone after a particular
amount of time. For example, think about flying from JFK to LHR;
how far have you traveled in 4.5 hours etc.
Call x the time measured in hours,
and y the distance you have
traveled measured in kilometers (km).
Then the function y = f(x)
simply relates time flown to distance traveled.

- Question: how do you interpret the derivative of f?

- Interpretations come from looking at the units of measurement.

- What are the units of the derivative?

- The derivative is a ratio; change in y over change in x.

- If y is measured in km, then a change in y must be measured in
km too.

- If x is measured in hours then a change in x must be measured in
hours.

- So the derivative has units km/hour,
that is kilometers per hour.

- So the derivative is simply speed or velocity - how fast you are going.

- Challenge: what's the derivative of velocity with respect to time?



Next: 4.2
Up: 4.
Previous: 4.
Richard Waterman
1999-06-01
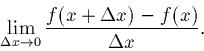
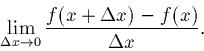
![]() gets smaller and smaller, how much does y change, and what
about the slope, that is the ratio of
gets smaller and smaller, how much does y change, and what
about the slope, that is the ratio of
![]() ?
?
![]() .
Note the lower case
d's rather than the
.
Note the lower case
d's rather than the ![]() 's.
's.