7.2 The chain rule - rule for a composition of functions

Take a function f(x), and another, g(t) where x = g(t), then the composition of the functions, f and g, is written as f(g(t)).

This happens when the result of one process is the input for another. Recall the function boxes from class 1.

Example:

$$f(x) = x^2 \qquad\qquad x = g(t) = 3\, t + 2.$$

$$f(g(t)) = (3\,t + 2)^2.$$

First apply g, then apply f to g itself.

The chain rule.

$$\frac{d}{dt} f(g(t)) = \frac{df}{dg} \times \frac{dg}{dt} = f'(g(t)) \times g'(t).$$

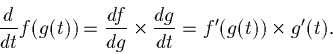
Example: differentiate (e^t)³.

Call e^t, x. Then

$$f(x) = x^3 \qquad\qquad x = g(t) = e^t.$$

$$f' = 3\,x^2 \qquad\qquad g' = e^t.$$

$$\frac{d}{dt} f(g(t)) = \frac{df}{dg} \times \frac{dg}{dt} = f'(g(t)) \times g'(t).$$

$$3\,(e^t)^2 \times e^t = 3\,(e^t)^3 = 3\,e^{3\,t}.$$

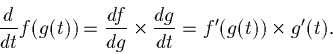
We will practice these more next class