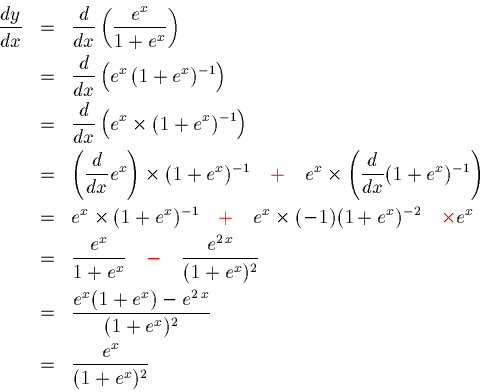3. Warm up examples

Two examples: one for products and another for the the chain rule.

Chain rule. We saw this last time. Most often used in the following context: A function inside parenthesis, raised to a power. Then the chain rule gives:

Bring down the power, knock the power down one, multiply by the derivative of what's in the parenthesis.

You have seen the cost function example many times, it shows how costs depend on the driver:

$$\mbox{\rm Cost} = 20 \, D^{0.9}.$$

Consider how the driver (labor hours) may depend on the number of units produced, call that U.

For example, $D = 100 + 0.25 \,U$.

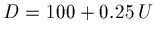Aside: interpret the 100 and 0.25 in the equation.

Substituting in D to the cost equation we can express the cost in terms of the number of units produced: we have

$$\mbox{\rm Cost} = 20 \, (100 + 0.25\,U)^{0.9}.$$

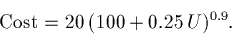
Now the question is ``what's the marginal cost with respect to the number of units produced''?

That is find $\frac{dC}{dU}$.

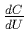Notice that this is a function raised to the power; it calls for the chain rule:

Bring down the power, knock the power down one, multiply by the derivative of what's in the parenthesis.

$$\frac{dC}{dU} = 20 \times 0.9 \times (100 + 0.25\,U)^{-0.1} \quad \times \quad 0.25.$$

Recall the propensity to repeat purchase model.

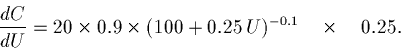
The simplest case for this model is, y = e^x/(1 + e^x), the S-shaped curve. Finding the derivative tells us at what rate the function is increasing. We might be interested in where it is increasing the fastest. Differentiate this function

$$\begin{eqnarray*}\frac{dy}{dx} & = & \frac{d}{dx} \left(\frac{e^x}{1 + e^x}\righ... ...e^x) - e^{2\,x}}{(1 + e^x)^2} \\ & = & \frac{e^x}{(1 + e^x)^2} \end{eqnarray*}$$

You, sketch this curve: where is the derivative largest?