MathCamp98. Class 1

Applications

Series and limits - asymptotes with time, product saturation.

Comparisons in a portfolio.

Exponents - exponential growth - cellular example.

Logistic curves - modeling failure probabilities.

Logs - natural, base e, transforming prices into returns.

Log transforms compare like with like - the exec pay compensation. Base_10 has an interpretation too.

Log-Log relationships. Elasticity interpretations.

Today's class

Some basic notation - summation and powers

Exponents

Factorials

E

Logs

Summation notation

Sum the numbers 1 to 100.

Symbolically, call the sum T,

Generally

.

Answer indicates how the sum depends on n.

How do we get the answers? Pictures often help.

The ideas of raising to a power (initially geometric):

• is just n
• or n-squared
• or n-cubed

Where is this useful to know?

How many comparisons between 8 test products - pairwise comparisons.

How many two way relationships between 198 stocks in a portfolio - covariances

Extra:

What could T(m,n) mean?
Find an expression for T(m,n) in terms of T(1,m) and T(1,n) when .

A few more series - illustrating limits.

General exponents

What does mean? The BASE is y and the EXPONENT is m.

For m an integer

From this simple definition we get

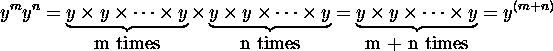
Key fact: multiplication of numbers turns into addition of their exponents.

must be equal to 1.

Golden rule: anything raised to the power 0 equals 1.

so that must equal .

is the number which when multiplied by itself gets you back y - the definition of the square root.

In general is called the m-th root of y. If you think this is going out to lunch consider cellular phone use in the US.

More rules:

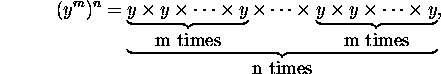
Finally

Golden rules for exponents:

1. .
2. 
3. .
4. 
5. .
6. 

Factorials

This is the exclamation mark notation (!).

Define 0! as 1. Define n! as .

Then

These things get big fast.

They show up all over the place, approximation formulae and combinatorics.

Question: how many ways can I choose 3 distinct stocks from a portfolio of 8? Answer:

A special series that involves factorials:

Equals e = 2.718281828459....

e

This is one of those magical numbers like . We see it in continuous compounding - exponential growth - entities that grow like .

Look at a graph of e to the power t.

Logarithms

Think of logarithms as exponents going backward (inverses).

To what power do I have to raise a to get to y.

In other words

The question marks are defined as the logarithm of y base a.

Examples

In English: to what power do I have to raise 10 to get 1000?

The logarithm of 1000 base 10 is 3.

So logarithms to base 10 can be used to summarize variables into magnitude ``bins'', for example the Executive Compensation.

Addressable memory examples.

Logarithms to base 2. Everything to do with computers.

The logarithm of 256 base 2 is 8.

With eight bits you can represent 256 different numbers.

The logarithm of 65536 base 2 is 16.

The logarithm of 4,294,967,296 base 2 is 32.

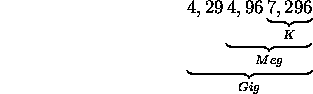
So a 32 bit operating system has 4 gigs of addressable memory.

Log facts:

The log of product is the sum of the logs.

A special base for logs is the log base e. Written as ln.

So

Taking logs undoes exponentiation.

A very useful fact to be explained later:

For small values of h

Say we have increases of sales of 1%. That is . So

Therefore the difference in logs:

So the difference in logs gets interpreted as a ``percent change'' for small changes.

Summary of class.

Introduced notation. Summation, exponentiation

Discussed exponents, factorial and logs

Homework questions.

A set of quick questions to reinforce the days concepts. A calculator will often be needed.