6.2 Example: compounding investments

Next: 6.3 Turning the question Up: 6. Functions of more Previous: 6.1 Introduction

6.2 Example: compounding investments

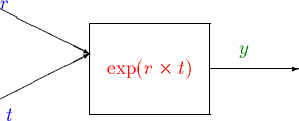
Later in the course we will study continuous compounding, which among other things can be used to describe how money grows over time. If one dollar is initially invested, then at a later date, say t years in the future, if the interest rate is r, it grows according to the rule

Money at time t equals exp(r t), where exp stands for the exponential function.

This relationship can be represented graphically as

$\begin{picture}(12,4) \put(1,4){\vector(2,-1){3}} \put(1,4.0){\textcolor{blue}{$... ... \put(8,2){\vector(1,0){3}} \put(9,2.5){\textcolor{green4}{ $y$ }} \end{picture}$

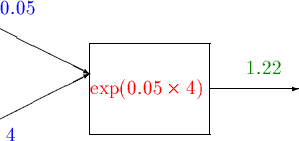
Suppose the interest rate is 5%, and that the dollar is invested for 4 years, then r = 0.05 and t=4 giving

$\begin{picture}(12,6) \put(1,4){\vector(2,-1){3}} \put(1,4.5){\textcolor{blue}{ ... ...ut(8,2){\vector(1,0){3}} \put(9,2.5){ \textcolor{green4}{$1.22$ }} \end{picture}$

Symbolically we write

$\begin{displaymath}\fbox{$ \mbox{\rm Value} = f(r,t)$ }\end{displaymath}$

which displays the fact the the value of the investment, y, depends on two quantities, r the interest rate and t, the length of time that the investment is held.

Next: 6.3 Turning the question Up: 6. Functions of more Previous: 6.1 Introduction

Richard Waterman
1999-04-30