3.2 Definitions and rules

The ideas of raising to a power (initially geometric):

n¹ is just n

$n^2 = n \times n$ or n-squared

$n^3= n \times n \times n$ or n-cubed

Some examples of power relationships. Where is this useful to know?

How many comparisons between 4 test products - pairwise comparisons?

How many pairwise relationships between 198 stocks in a portfolio - covariances?

Both of these depend on square of the number of items (products/stocks) - parabolic.

Defining y^m.

The base is y and the exponent is m.

For m an integer (whole number)

$$\fbox{$y^m = \underbrace{y \times y \times \cdots \times y }_{\mbox{\rm m times}}.$ }$$

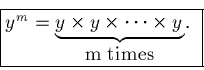
Example:

$$\fbox{$ 3^4 = \underbrace{3 \times 3\times 3 \time 3 \times 3 }_{\mbox{\rm 4 times}} = 81.$ }$$

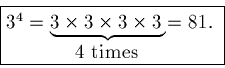
From this simple definition we get

$$\fbox{$y^m \, y^n = \underbrace{y \times y \times \cdots \tim... ...imes \cdots \times y }_{\mbox{\rm m + n times}} = y^{(m+n)}.$ }$$

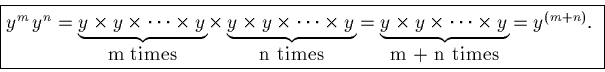
Example:

$$\fbox{$ 2^2 \times 2^3 = 2^{2 + 3} = 2^5 = 32.$ }$$

Key fact: multiplication of numbers becomes addition of their exponents.

A special case:

$$\fbox{$y^m \times y^0 = y^{m + 0} = y^m.$ }$$

It follows that y⁰ must be equal to 1.

Golden rule: anything raised to the power 0 equals 1.

$$\fbox{$y^m \times y^{-m} = y^{m + (-m)} = y^0 = 1,$ }$$

so that y^-m must equal $\frac{1}{y^m}$.

Fractional exponents:

$$\fbox{$y^{\frac{1}{2}} \times y^{\frac{1}{2}} = y^{\frac{1}{2} + \frac{1}{2}}\ = y^{1} = y,$ }$$

$y^{\frac{1}{2}}$ is the number which when multiplied by itself gets you back y - the definition of the square root.

In general $y^{\frac{1}{m}}$ is called the m-th root of y.

Recall cellular phones again where we used a fourth root transformation.

Cell phone subscribers

Transformed subscribers.

More rules:

$$\fbox{$(y^m)^n = \underbrace{ \underbrace{y \times y \times \... ...cdots \times y }_{\mbox{\rm m times}}}_{\mbox{\rm n times}},$ }$$

so that

$$\fbox{$(y^{m})^n = y^{m\,n}.$ }$$

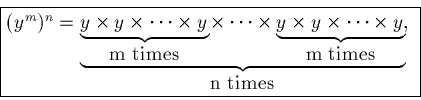
Example

$$\fbox{$(2^3)^2 = \underbrace{ \underbrace{2 \times 2 \times 2... ...rm 3 times}}}_{\mbox{\rm 2 times}} = 8 \times 8 = 64 = 2^{6}$ }$$

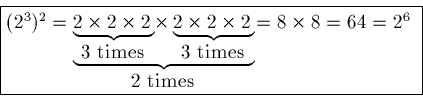
Finally

$$y^{\frac{n}{m}} = (y^{n})^{\frac{1}{m}}.$$

Golden rules for exponents:

1.

y^m yⁿ = y^{(m + n)}.

2.

$y^{-m} = \frac{1}{y^m}.$

3.

$\frac{y^m}{y^n} = y^m y^{-n} = y^{m - n}$.

4.

$(y^m)^n = y^{m\,n}.$

5.

$(y\, x)^m = y^m x ^m$.

6.

$(\frac{y}{x})^m = \frac{y^m}{x^m}.$