


Next: 5.
Up: Business
Previous: 3.3
This is one of those magical numbers like 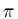 .
We see it in continuous
compounding - exponential growth - entities that grow like
.
We see it in continuous
compounding - exponential growth - entities that grow like 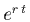 .
Sometimes called the ``base of natural logarithms'',
.
Sometimes called the ``base of natural logarithms'',
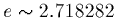 .
.
Look at a
graph.
of e to the power t,
et = exp(t).
Notes

- Defined for all values of t, even negative ones.

- Crosses that y-axis at y = 1, why?

- This relationship really grows fast, hence the term
exponential growth.

- As t heads to negative infinity, et goes to 0.

- As t heads to positive infinity, et goes to infinity.
Why don't we call this a power function?
Because the object we are changing, t, is in the exponent,
not the base.
The more general form of the function:
Here

- C is a multiplicative constant (how much money at the start).

- e is the magical number.

- r is a fixed constant (the interest rate).

- t is what we are changing (how long the investment is held for).
Example.

- C = 100.

- r = 0.05 is a fixed constant (the interest rate).

- t is time in years.
Rules for exponential functions (same as power functions):

-
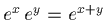 .
.

-
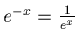 Exponential decay.
Exponential decay.
A useful modeling function: the logistic:
This is in fact the formula for the
graph.



Next: 5.
Up: Business
Previous: 3.3
Richard Waterman
1999-05-06
![]() .
We see it in continuous
compounding - exponential growth - entities that grow like
.
We see it in continuous
compounding - exponential growth - entities that grow like ![]() .
Sometimes called the ``base of natural logarithms'',
.
Sometimes called the ``base of natural logarithms'',
![]() .
.