5.2 Continuous compounding

Subscripting notation: the small t.

Percentage changes. 5% growth means multiply by 1.05

Example. Take $1,000 and compound it annually at 5%.

Call the principle P₀, the amount of money you have at time zero.

 

Table 3: A table of yearly compounded results of an initial investment of $1000

Year (t)	Amount (Pt)
0	1000
1	$1000 + 0.05 \times 1000 = 1000 \times(1 + 0.05) = 1000 \times 1.05 = 1050$
2	$1050 + 0.05 \times 1050 = 1050 \times(1 + 0.05) = 1050 \times 1.05 = 1102.5$
3	$1102.5 + 0.05 \times 1102.5 = 1102.5 \times(1 + 0.05) = 1102.5 \times 1.05 = 1157.625$
t	$P_{t-1} \times 1.05 = P_0 \times 1.05^t$

In general

$$\fbox{$P_t = P_0 (1 + r)^t,$ }$$

where r is the interest rate per period and t is the number of compoundings.

In the above example, interest was compounded once per year. One can compound more frequently. What difference does it make? How do we set it up?

If the annual interest rate is r and it is compounded m times in a year then the rate per period is $\frac{r}{m}$.

$$\fbox{$ \mbox{\rm Rate per period } = \frac{r}{m}.$ }$$

Example, if the annual rate is 5% and this is compounded quarterly then the rate per quarter is $\frac{0.05}{4} = 0.0125$.

 

Table 4: An annual nominal 5% interest rate, compounded over a variety of periods.

Period	Number of periods	Rate per	Nominal	Effective
	in year	period	annual rate	annual rate
1 year	1	0.05	0.05	0.0500
1 quarter	4	$\frac{0.05}{4}$	0.05	0.0509
1 month	12	$\frac{0.05}{12}$	0.05	0.0512
1 day	250	$\frac{0.05}{250}$	0.05	0.0512

Where do the numbers come from? Example, the quarterly compounding.

The rate per period is 0.05/4 = 0.0125. So we have an increase of a factor of (1 + 0.0125)⁴ = 1.0509, an increase of 5.09%.

Conclusion: you do a little bit better if the principle is more frequently compounded, but it reaches a limit fast.

In general: have an annual rate r compounded m times a year. The rate per period is $\frac{r}{m}$. How much do you have at the end of t years?

How many compoundings total? m times a year for t years makes $m\,t$ compoundings. Rate per period is $\frac{r}{m}$ so the formula gives

$$P_t = P_0 \left(1 + \frac{r}{m}\right)^{m\, t}.$$

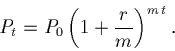
Now the calculus part: let m get large. That is compound more and more frequently (but a smaller rate during each interval).

Consider the limit:

$$\lim_{m \rightarrow \infty} P_0 \left(1 + \frac{r}{m}\right)^{m\, t}.$$

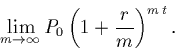
Answer:

$$\lim_{m \rightarrow \infty} P_0 \left(1 + \frac{r}{m}\right)^{m\, t} = P_0 \, e^{r\,t}.$$

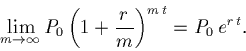
So that the number e comes in naturally as a limit in continuous compounding.