5.3 Examples

How long does it take a principle amount to double if the interest rate is $4\%$?

Principle is P₀.

Principle has doubled when amount at time t equals twice the principle.

That is $P_t = 2 \times P_0$.

So the question is, what value of t (how long) makes P_t double P₀?

The formula for continuous compounding states that $P_t = P_0 \, e^{rt}$, so the question is now ``what value of t makes $P_0 \,e^{rt} = 2 \, P_0$''?

Some simplifications (trying to get at t):

$$\begin{eqnarray*}P_0 e^{rt} & =& 2 \, P_0 \\ e^{rt} &= & 2 \qquad \mbox{\rm c... ...& \frac{ln(2)}{r} \qquad \mbox{\rm divide through by $r$ .} \\ \end{eqnarray*}$$

So the doubling time is ln(2)/r and this does not depend on the principle P₀.

In particular for r equal to 4% or 0.04 we get ln(2)/0.04 = 17.329.

Always check the answers: Say P₀ is 1000.

Then

$$1000\, e^{0.04 \times 17.329} = 1000\, e^{0.69316} = 1000 \times 2.0000256.$$

So, it has indeed doubled (up to rounding error).

Next example:

A invests $1000 at 5% per annum continuously compounded.
B invests $200 at 20% per annum continuously compounded.

Questions? Does B ever catch up? How long does it take?

B catches up if the difference between them becomes zero.

Alternatively if the ratio of their amounts becomes 1.

Equality can be expressed as a difference of zero or as a ratio of one.

Draw a picture using a graphing package .

When does it happen: either approximate from the graph or work out explicitly once and for all.

A has at time t, $1000\, e^{0.05 \, t}$.

B has at time t, $200\, e^{0.20 \, t}$.

The equality condition can be stated as:

$$\frac{1000\, e^{0.05 \, t}}{200\, e^{0.20 \, t}} = 1.$$

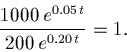
Solve this for t again.

$$\begin{eqnarray*}\frac{1000}{200} \frac{e^{0.05 \, t}}{e^{0.20 \, t}} & = & 1. \... ....15}.\\ t & = & 10.73 \qquad\qquad \mbox{\rm Calculate it!}. \end{eqnarray*}$$

So it takes about 11 years for B to catch up.