


Next: 6.
Up: 5.
Previous: 5.3
Where does the continuous compounding formula come from?
Assume the limit exists, and call it L, then:
So
If we are allowed ...
Now, log of a product is the sum of the logs ...
Use log rules:
But as m gets large, so
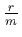 gets really small, so can use the
log approximation
gets really small, so can use the
log approximation
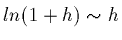 ,
to get
,
to get
Cancel to get
Now exp both sides to get



Next: 6.
Up: 5.
Previous: 5.3
Richard Waterman
1999-05-14
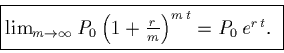
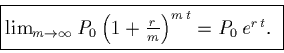
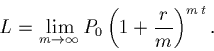
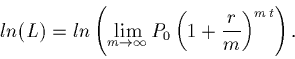
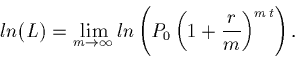
![\begin{displaymath}ln(L) = \lim_{m \rightarrow \infty}\left(ln(P_0) + ln \left[\left(1 + \frac{r}{m}\right)^{m\, t}\right]\right).\end{displaymath}](img68.gif)