


Next: 4.4
Up: 4.
Previous: 4.2

- The derivative of a constant is 0. If
y = f(x) = 6, then
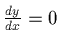 .
Ask yourself the question ``how does a constant change as x changes?''
.
Ask yourself the question ``how does a constant change as x changes?''

- For y = xn,
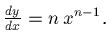 "Bring down the power, knock the power down 1."
"Bring down the power, knock the power down 1."

- Examples:

- The derivative of x4 is
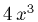 .
.

- The derivative of x-2 with respect to x,
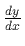 ,
is
,
is
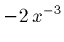 .
.

- The derivative of a sum is the sum of its derivatives.

- Examples

-
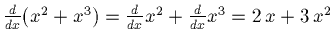 .
.

-
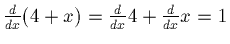 .
.

- If c is a constant then
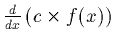 is equal to
is equal to
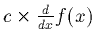 .
.
That, is the derivative passes through a constant
multiple.

- Examples

-
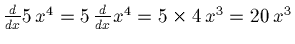 .
.

- The derivative of a straight line must be its slope:
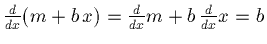 .
.

- For y = ex
the derivative with respect to x,
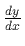 ,
is ex.
,
is ex.

- For
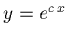 the derivative with respect to x,
the derivative with respect to x,
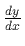 ,
is
,
is
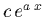 .
.

- For y = ln(x) the derivative with respect to x,
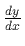 ,
is
,
is
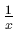 .
.



Next: 4.4
Up: 4.
Previous: 4.2
Richard Waterman
1999-06-01

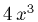 .
.

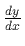 ,
is
,
is
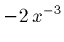 .
.

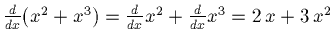 .
.

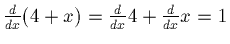 .
.

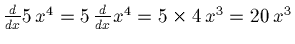 .
.

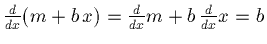 .
.