4.4 Example

An example cost function:

$$\mbox{\rm Cost} = C \, D^{\beta_1}.$$

D here is termed a ``cost driver''. Changes in the cost driver impact cost.

Take C = 20, then

A simple question: how much does cost change for a small (one unit) change in the driver, D?

This is the definition of the marginal cost.

For example, the driver D could be labor hours. If $\beta_1$ equals 1 then the equation is (anything to the power one is itself)

$$\mbox{\rm Cost} = 20 \, D.$$

The left-hand side is measured in Dollars, D is measured in hours, so to make things balance C must be in dollars/hour, ie a wage rate.

Consider what happens if $\beta_1 = 0.9$, so that

$$\mbox{\rm Cost} = 20 \, D^{0.9}.$$

Find the marginal cost at D = 100.

First differentiate; bring down the power, knock the power down 1, to get:

$$\frac{dC}{dD} = 20\times 0.9 \,D^{-0.1},$$

and evaluate this at D = 100, to find that the marginal cost is $11.357. That is, if the driver increases by 1 unit (purchase an additional labor hour) then costs should increase by about $11.

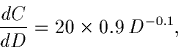
What about the marginal cost at D = 200? You calculate to find that the marginal cost is 10.60.

Note how the marginal cost is decreasing as the driver increases.

Homework question: plot this marginal cost function for D = 50,100,150,200, 250, 300.