5. Liquor store example

Data collected from a set of liquor stores captures the relationship between shelf space devoted to a new product and the sales generated by the product.

There is an alternative product that can guarantee sales of $50 for each foot of shelf space.

How much shelf space should be devoted to the new product in order to maximize sales?

Two alternative specifications for the relationship, call S the sales, and L then length of shelf space:

$S = 85.56 + 138.62 \times ln(L).$

$S = -12.40 + 108.77\,L - 8.49\,L^2$

What are their implications?

Look at the derivatives:

For the log relationship we have

$$\fbox{$\frac{dS}{dL} = 138.62 \times \frac{1}{L} = \frac{138.62}{L},$ }$$

and for the quadratic:

$$\fbox{$\frac{dS}{dL} = 108.77 - 8.49 \times 2\, L = 108.849 - 16.98 \,L.$\space }$$

Questions: is the derivative positive or negative, and at which values of L. How does the Sales function behave as the number of shelf feet changes?

The log is increasing for all values of L, whereas the quadratic reaches a maximum and then starts to fall.

We will go with the log.

Key question: how many shelf feet to allocate to the new product?

Logically, under what condition would you add an additional foot?

Answer; only add an additional foot if it generates more than $50 in sales, because if it didn't you would substitute the alternative product.

So you keep adding shelf feet until the incremental foot, adds less than $50 in sales.

Incremental foot means change in L. Adding $50 in sales means change in S. So the $50, cut off factor, represents the change in S to the change in L, but that is just the derivative of S with respect to L.

The solution is to add shelf feet, until the derivative of the sales function with respect to shelf feet is less than 50.

So we will solve this equation:

Keep adding shelf feet until derivative of S with respect to L equals 50.

$$\begin{eqnarray*}\frac{dS}{dL} &=& \frac{138.62}{L} \\ \frac{138.62}{L} &=& 50 \\ 2.77 &=& L \\ \end{eqnarray*}$$

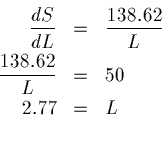
So we need about two and three quarter feet of the new product to maximize sales.