6. Cost function example

Recall last class' cost function example:

$$\mbox{\rm Cost} = 20 \, D^{\beta_1}.$$

D here is termed a ``cost driver''. The costs are denoted by C. (This is a slight change in notation from last class). Changes in the cost driver impact cost.

Putting in a specific value for $\beta_1$ then,

$$\mbox{\rm Cost} = 20 \, D^{0.9}.$$

What do we learn about this function?

Is it increasing with respect to D?

Look at the derivative.

At what rate is it in increasing.

Note that it increases, at a decreasing rate.

Thought question:

Recall percentage change: $\frac{\Delta x}{x}$.

In this context, percentage change in the driver is $\frac{\Delta D}{D}$.

Percentage change in costs is $\frac{\Delta C}{C}$.

How does percent change in the driver relate to percent change in the costs? We would like to say that if the driver changes by a certain percentage then the costs change by such and such a percentage.

Look at the ratio of percent changes:

$$\fbox{$\frac{ \frac{\Delta C}{C}}{\frac{\Delta D}{D}} = \frac{\Delta C}{\Delta D} \times \frac{D}{C}.$ }$$

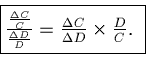
Now recall the definition of the derivative: the ratio of the changes, as the changes become small.

Letting the percent change become small the quantity:

$$\fbox{$ \frac{dC}{dD} \times \frac{D}{C},$ }$$

is called the elasticity of costs with respect to the driver (the elasticity of C with respect to D).

Work out the elasticity now for the cost function example.

$$\frac{dC}{dD} = \frac{d}{dD}\left(20 \, D^{0.9}\right) = 18\,D^{-0.1}.$$

$$\frac{D}{C} = \frac{D}{20\,D^{0.9}} = \frac{1}{20}\,\frac{D^1}{D^{0.9}} = \frac{1}{20}\,D^{1 - 0.9} = \frac{1}{20}\, D^{0.1}.$$

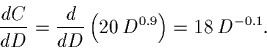
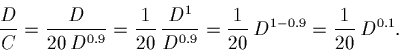
So the elasticity equals:

$$\frac{dC}{dD} \times \frac{D}{C} = (18\, D^{-0.1}) \times \left( \frac{1}{20} D^{0.1}\right) = 0.9.$$

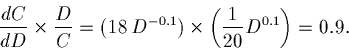
The interpretation is that the ratio of the percent changes is 0.9, so a 1% change in the driver results in a 0.9% change in the costs. Notice that 0.9 is the power in the original cost function - so that the power is interpreted as the elasticity.

The key point with this cost function, is that the elasticity is a constant, it doesn't depend on the level of the driver.

Straight lines are characterized by a constant slope.

Power relationships are characterized by a constant elasticity.