4.2 Variances

Variance measures how spread out a distribution is. It is the key ,easure of risk. It is defined by

$$\fbox{$Var(X) = E(X^2) - E(X) E(X)$ .}$$

How do we find the average of X²?

 

Table 3: Returns squared distribution for Air.com

Return.Squared	9	4	1	0	1	4	9
Probability	0.2	0.1	0.05	0.05	0.1	0.2	0.3

$$\begin{eqnarray*}E(X^2) & = & \textcolor{red}{0.2} \times \textcolor{blue}{9}\qu... ...tcolor{red}{0.3} \times \textcolor{blue}{9}\quad \\ & = & 5.85 \end{eqnarray*}$$

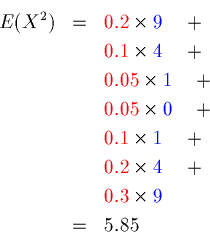
This implies that the variance is given by

$$Var(X) = 5.85 - 0.55 \times 0.55 = 5.5475.$$

What happens to a multiplicative constant, times our variable of interest? Here is an example where we look at 3 times the variable.

$$\begin{eqnarray*}Var (3\,X) &=& E((3X)^2) - E(3 X) E(3 X) \\ Var (3\,X) &=& E(9... ... (3\,X) &=& 9 ( E(X^2) - E(X) E( X))\\ Var (3\,X) &=& 9 Var (X) \end{eqnarray*}$$

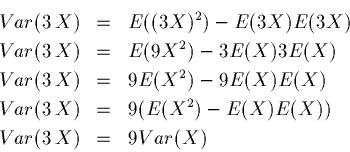
So in general, with a weight w we have

$$Var (w\,X) = w^2\,Var(X).$$

You find the mean and variance of Bricks.