5. Summarizing joint probability distributions

The main measure is called covariance. It measures the strength of the linear relationship between two variables and is defined as

$$\fbox{$Cov(X, Y) = E(X\, Y) - E(X) E(Y). $ }$$

Notice that $Cov(X,X) = E(X\, X) - E(X) E(X) = Var(X)$, so that variance is simply the covariance of a variable with itself.

Covariance tells us how 2 variables are associated, so we need the joint distribution of the variables. Take the following table as a given.

 

Table 4: The joint probability distribution of returns on Air.com and Bricks

	Bricks (Y)
Air.com (X)	-3	-2	-1	0	1	2	3	Total
-3	0.030	0.0200	0.045	0.06	0.015	0.020	0.0100	0.2
-2	0.005	0.0300	0.010	0.03	0.010	0.010	0.0050	0.10
-1	0.000	0.0025	0.025	0.01	0.005	0.005	0.0025	0.05
0	0.005	0.0075	0.000	0.03	0.000	0.005	0.0025	0.05
1	0.010	0.0150	0.025	0.02	0.025	0.000	0.0050	0.10
2	0.020	0.0300	0.040	0.06	0.010	0.040	0.0000	0.20
3	0.030	0.0450	0.055	0.09	0.035	0.020	0.0250	0.30
Total	0.10	0.15	0.20	0.30	0.10	0.10	0.05	1.00

Recall that X is the return on Air.com and Y is the return on Bricks.

We know that E(X) = 0.55. You worked out that E(Y) = -0.35.

We must find $E(X\,Y)$. It is the same rule as before but now we find the weighted average of X times Y. The weights are the joint probabilities. This could be a messy calculation as there are 49 of them in this example!

But it starts like this:

$$\begin{eqnarray*}E(X\,Y) & = & \textcolor{red}{0.030} \times \textcolor{blue}{-3... ...} \times \textcolor{blue}{-3 \times 2} \quad + \\ & & \cdots + \end{eqnarray*}$$

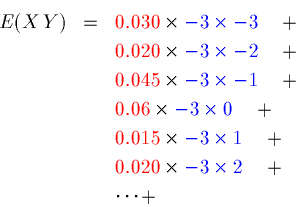
and ends:

$$\begin{eqnarray*}& & + \textcolor{red}{0.045} \times \textcolor{blue}{3 \times -... ...imes \textcolor{blue}{3 \times 3} \quad + \\ & = & -0.0825 \\ \end{eqnarray*}$$

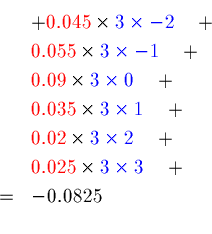
So that $E(X\,Y) = -0.0825$.

That means that $Cov(X,Y) = -0.0825 - (0.55)\times(-0.35)= 0.11$.

Fact: if 2 random variables are independent then their covariance is zero.

Formula:

$$\framebox{$E(X\,Y) = \sum_{\textcolor{blue}{x}}\sum_{\textcol... ...x \quad \mbox{\rm and} \quad Y = y)} \textcolor{blue}{x\,y}$ }$$

The double summation, indicates that we are summing elements that lie in a table. Think of them as rows and columns.